Министерство Образования и Науки Украины

Национальный Технический Университет Украины «Киевский Политехнический Институт»

Учебно-научный комплекс «Институт Прикладного Системного Анализа»

Кафедра «Математических Методов Системного Анализа»

Курсовая работа

По предмету «Теория Управления»

Выполнил:

Студент 4 курса

Группы КА-81

Верещагин Павел

Принял:

Романенко Виктор Демидович

Киев-2010

Исходные данные:

K	T1	T2	T3	τ
3.87	52	31	11	17

1.Расчет импульсной передаточной функции замкнутого контура нцу

Сначала определим импульсную передаточную функцию приведенной непрерывной части:

Дискретная передаточная функция замкнутого контура НЦУ по каналу «задание регулятора – выходная регулирующая переменная» определяется как:

,

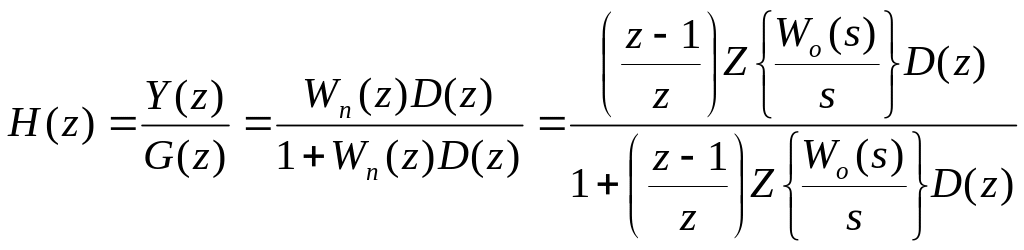где - Z- преобразование от задающего воздействия, - соответственно Z- преобразование от выходной регулируемой координаты.

Рассмотрим импульсные функции для регуляторов.

Импульсная передаточная функция ПИД регулятора:

Импульсная передаточная функция ПИ регулятора:

1.1 Расчет для объекта 1 без задержки:

Для ПИД регулятора импульсная передаточная функция замкнутого контура имеет вид:

Для ПИ регулятора импульсная передаточная функция замкнутого контура имеет вид:

1.2 Расчет для объекта 2 без задержки

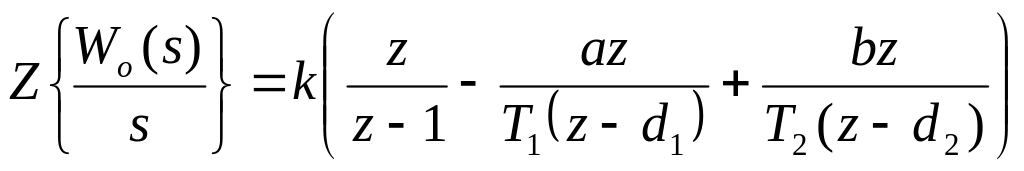
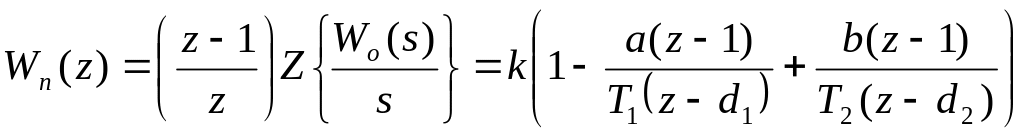
Для ПИ регулятора импульсная передаточная функция замкнутого контура имеет вид:

Для ПИД регулятора импульсная передаточная функция замкнутого контура имеет вид:

1.3 Расчет для объекта

при

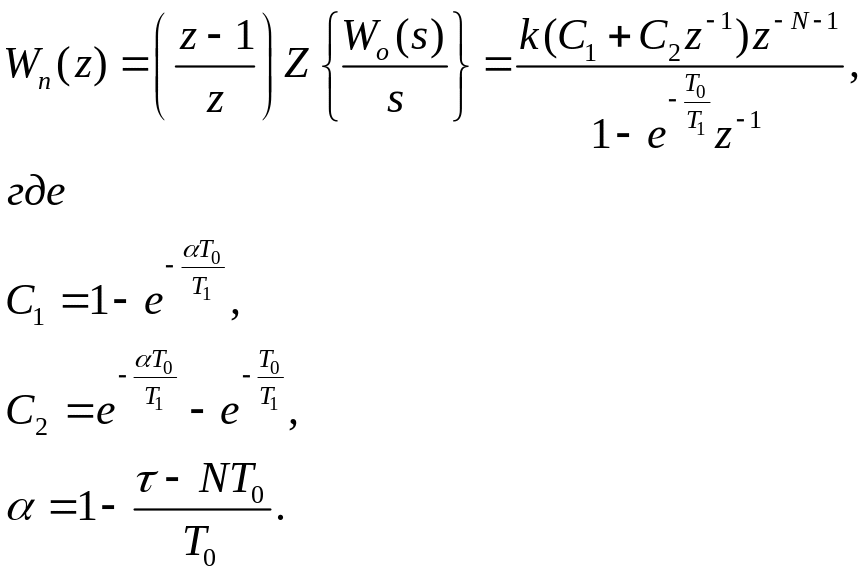
Параметр N равняется наибольшему числу от деления времени запаздывания на период квантования .

Для ПИ регулятора импульсная передаточная функция замкнутого контура имеет вид:

Для ПИД регулятора импульсная передаточная функция замкнутого контура имеет вид:

1.4 Расчет для объекта

при

_{Откуда получаем:}

Для ПИ регулятора импульсная передаточная функция замкнутого контура имеет вид:

Для ПИД регулятора импульсная передаточная функция замкнутого контура имеет вид:

2. Расчет периода квантования в системе нцу.

2.1. Метод, основанный на обеспечении точности управления.

Введем понятие степень неопределенности объекта относительно его регулироемой координати в момент времени : . Область неопределенности должна быть ограничена постоянным значением . Если разложить выражения в ряд Тейлора с точностью до первой производной и учесть условие метода, что неопределенность информации должна быть меньше заданной точности, получим следующее выражение: . Решаем неравенство аналитически и получаем:

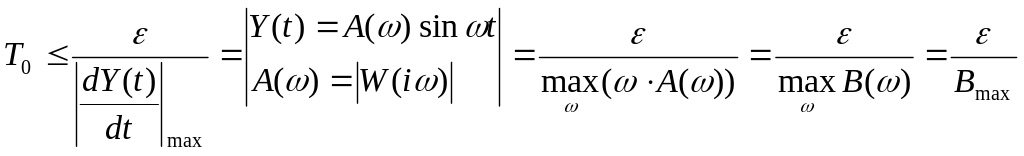
В – характеристика, что интерпретируется, как верхняя граница возможных или ожидаемых изменений скорости на выходе объекта.

Поэтому в данном пункте курсовой работы мы находим . А далее рассчитываем период квантования для каждого заданного значения ε по формуле:

.