
- •Скалярное произведение векторов. Его основные свойства.
- •. Выражение скалярного произведения в координатах
- •Смешанное произведение векторов
- •7. Преобразование прямоугольных координат при повороте осей.
- •8. Линии на плоскости. Понятие уравнения линии.
- •9. Уравнение линии в полярной системе координат.
- •10. Параметрическое уравнение линии
- •11. Векторное уравнение линии.
- •12. Алгебраические линии.
- •13. Линии первого порядка.Уравнение прямой с угловым коэффициентом.
- •14.Уравнение прямой. Проходящей через данную точку, имеющей заданный угловой коэффициент.
- •15. Уравнение прямой, проходящей через две точки.
- •16.Общее уравнение прямой.
- •17Уравнение прямой в отрезках.
- •18. Каноническое уравнение прямой на плоскости.
- •19. Угол между двумя прямыми. Условие параллельности и пе4. Условия параллельности двух прямых:
- •20. Расстояние от точки до прямой на плоскости.
- •21. Линии второго порядка на плоскости.
- •22. Эллипс. Вывод канонического уравнения эллипса.
- •23. Векторное уравнение эллипса.
- •24. Гипербола .Вывод канонического уравнения гиперболы
- •25. Парабола. Вывод канонического уравнения параболы.
- •26. Общие уравнения линии второго порядка
23. Векторное уравнение эллипса.
24. Гипербола .Вывод канонического уравнения гиперболы
25. Парабола. Вывод канонического уравнения параболы.
Пусть
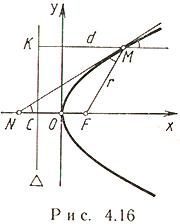
на плоскости заданы точка F и прямая![]() , не проходящая через F. Парабола -
множество всех тех точек M плоскости,
каждая из которых равноудалена от точки
F и прямой
. Точка F называется фокусом, прямая
- директрисой параболы; (OF) - ось, O -
вершина,
, не проходящая через F. Парабола -
множество всех тех точек M плоскости,
каждая из которых равноудалена от точки
F и прямой
. Точка F называется фокусом, прямая
- директрисой параболы; (OF) - ось, O -
вершина,
![]() - параметр,
- параметр,
![]() - фокус,
- фокус,
![]() - фокальный радиус.
- фокальный радиус.
Каноническое
уравнение:
![]()
Эксцентриситет:
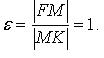
Фокальный
радиус:
![]()
Уравнение
директрисы:
![]()
Уравнение
касательной в точке
![]()
![]()
Свойство
касательной к параболе:
![]() (М - точка касания; N - точка пересечения
касательной с осью Ox).
(М - точка касания; N - точка пересечения
касательной с осью Ox).
Уравнение нормали в точке
![]()
Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.
Параметрические
уравнения параболы:
![]()
Полярное
уравнение:
![]()
26. Общие уравнения линии второго порядка
Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям
Найдем
сначала уравнение эллипса с центром в
точке![]() , оси симметрии которого параллельны
координатным осям Ох и Оу и полуоси
соответственно равны а и b. Поместим в
центре эллипса
, оси симметрии которого параллельны
координатным осям Ох и Оу и полуоси
соответственно равны а и b. Поместим в
центре эллипса![]() начало новой системы координат
начало новой системы координат![]() , оси которой
, оси которой
![]() и
и![]() параллельны соответствующим осям Ох
и Оу и одинаково с ними направленны (см.
рис.41).
параллельны соответствующим осям Ох
и Оу и одинаково с ними направленны (см.
рис.41).

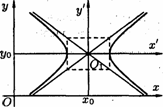 В
этой системе координат уравнение Рис.41.
В
этой системе координат уравнение Рис.41.
эллипса
имеет вид![]()
Так
как![]() , то в старой системе координат уравнение
эллипса запишется в виде
, то в старой системе координат уравнение
эллипса запишется в виде
![]()
Аналогично
рассуждая, получим уравнение гиперболы
с центром в точке
![]() и полуосями а и Ь (см. рис. 42):
и полуосями а и Ь (см. рис. 42):
![]()
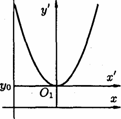
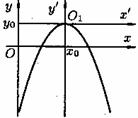
И, наконец, параболы, изображенные на рисунке 43, имеют соответствующие уравнения.

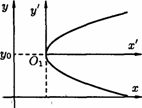
![]()
![]()
![]()
![]()
Уравнение Ac2 + Су2 + 2Dx + 2Еу + F = О
Уравнения
эллипса, гиперболы, параболы и уравнение
окружности![]() после преобразований (раскрыть скобки,
перенести все члены уравнения в одну
сторону, привести подобные члены, ввести
новые обозначения для коэффициентов)
можно записать с помощью единого
уравнения вида
после преобразований (раскрыть скобки,
перенести все члены уравнения в одну
сторону, привести подобные члены, ввести
новые обозначения для коэффициентов)
можно записать с помощью единого
уравнения вида
![]() (11.14)
(11.14)
где коэффициенты А и С не равны нулю одновременно.
Возникает вопрос: всякое ли уравнение вида (11.14) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка?
Ответ дает следующая теорема.
Теорема 11.2. Уравнение (11.14) всегда определяет: либо окружность (при А=С), либо эллипс (при А • С > 0), либо гиперболу (при А • С < 0), либо параболу (при АС = 0). При этом возможны случаи вырождения: для эллипса (окружности) - в точку или мнимый эллипс (окружность), для гиперболы - в пару пересекающихся прямых, для параболы - в пару параллельных прямых.
Пример
11.1. Установить вид кривой второго
порядка, заданной уравнением![]()
Решение:
Предложенное уравнение определяет
эллипс![]() . Действительно, проделаем следующие
преобразования:
. Действительно, проделаем следующие
преобразования:
![]()
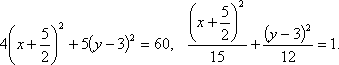
Получилось
каноническое уравнение эллипса с центром
в![]() и полуосями
и полуосями
![]() и
и![]() .
.
