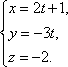- •Скалярное произведение векторов. Его основные свойства.
- •. Выражение скалярного произведения в координатах
- •Смешанное произведение векторов
- •7. Преобразование прямоугольных координат при повороте осей.
- •8. Линии на плоскости. Понятие уравнения линии.
- •9. Уравнение линии в полярной системе координат.
- •10. Параметрическое уравнение линии
- •11. Векторное уравнение линии.
- •12. Алгебраические линии.
- •13. Линии первого порядка.Уравнение прямой с угловым коэффициентом.
- •14.Уравнение прямой. Проходящей через данную точку, имеющей заданный угловой коэффициент.
- •15. Уравнение прямой, проходящей через две точки.
- •16.Общее уравнение прямой.
- •17Уравнение прямой в отрезках.
- •18. Каноническое уравнение прямой на плоскости.
- •19. Угол между двумя прямыми. Условие параллельности и пе4. Условия параллельности двух прямых:
- •20. Расстояние от точки до прямой на плоскости.
- •21. Линии второго порядка на плоскости.
- •22. Эллипс. Вывод канонического уравнения эллипса.
- •23. Векторное уравнение эллипса.
- •24. Гипербола .Вывод канонического уравнения гиперболы
- •25. Парабола. Вывод канонического уравнения параболы.
- •26. Общие уравнения линии второго порядка
15. Уравнение прямой, проходящей через две точки.
Если
прямая проходит через точки
![]() и
и
![]() ,
то ее направляющим вектором можно
считать вектор
,
то ее направляющим вектором можно
считать вектор![]() .
.
Уравнением
прямой, проходящей через две точки
и
называется уравнение вида![]()
В
случае, когда один из знаменателей равен
нулю (![]() соответствующий
числитель тоже равен нулю (
соответствующий
числитель тоже равен нулю (![]() :
:
если![]() , то прямая, проходящая через точки
и
, параллельна оси ординат и ее уравнение
имеет вид
, то прямая, проходящая через точки
и
, параллельна оси ординат и ее уравнение
имеет вид
![]()
если![]() , то прямая, проходящая через точки
и
, параллельна оси абсцисс и ее уравнение
имеет вид
, то прямая, проходящая через точки
и
, параллельна оси абсцисс и ее уравнение
имеет вид
![]()
Угловой
коэффициент прямой, проходящей через
две точки, находится по формуле![]()
Пример.
Составить уравнение прямой, проходящей
через точки![]() и
и
![]()
Решение.
![]()
или
![]() , так как
, так как
![]() ,
то прямая имеет уравнение
,
то прямая имеет уравнение
![]() ,
значит она параллельная оси ординат.
,
значит она параллельная оси ординат.
16.Общее уравнение прямой.
Общим уравнением прямой называется уравнение вида
![]()
Где
A,B,C
– произвольные числа, причем![]() .
.
Частные случаи:
Если
![]() и
и
![]() ,
то общее уравнение прямой имеет неполный
вид
,
то общее уравнение прямой имеет неполный
вид
![]() и
определяет прямую проходящую через
начало координат
и
определяет прямую проходящую через
начало координат
![]()
Если
![]() и
и
![]() ,
то
,
то
![]() и определяет прямую параллельную оси
и определяет прямую параллельную оси
Если
![]() и
, то
и
, то
![]() – прямая параллельная оси
– прямая параллельная оси
Если
![]() ,
то
,
то![]() прямая совпадает с осью .
прямая совпадает с осью .
Если
![]() ,то
,то![]() прямая совпадает с осью .
прямая совпадает с осью .
При![]() общее уравнение прямой
общее уравнение прямой![]() можно записать в виде:
можно записать в виде:
![]()
Пример.
Составить уравнение прямой, отсекающей
на оси ординат отрезок
![]() и образующей с положительным направлением
оси абсцисс угол
и образующей с положительным направлением
оси абсцисс угол![]() .
.
Решение.
Найдем угловой коэффициент![]() . Подставив в уравнение имеющиеся
значения , получим . Приравняем равенство
к нулю , избавимся от знаменателя для
чего умножим обе части равенства на ,
получим общее уравнение прямой .
. Подставив в уравнение имеющиеся
значения , получим . Приравняем равенство
к нулю , избавимся от знаменателя для
чего умножим обе части равенства на ,
получим общее уравнение прямой .
17Уравнение прямой в отрезках.
Преобразуем общее уравнение прямой следующим образом: перенесем в правую часть , разделим на получим получаем уравнением прямой в отрезках которое имеет вид:
![]() ,где
,где
![]() абсцисса
точки пересечения прямой с осью
абсцисса
точки пересечения прямой с осью
![]() ордината
точки пересечения с осью Оу .
ордината
точки пересечения с осью Оу .
Поэтому а и b называют отрезками прямой на осях координат.
Формулу![]() удобно использовать для построения
прямой.
удобно использовать для построения
прямой.
Для построения прямой достаточно взять две ее точки:
при![]()
Пример.
Составить общее уравнение прямой,
отсекающей на осях координат отрезки![]() ,
,
![]()
Решение.
Воспользовавшисьуравнением прямой в
отрезках![]() , имеем , перепишем его в виде
, имеем , перепишем его в виде![]() или
или
![]() .
.
Пример.
Составить уравнение прямой проходящей
через точку
![]() и отсекающей от координатного угла
треугольник площадью равной 2 кв.ед.
и отсекающей от координатного угла
треугольник площадью равной 2 кв.ед.
Решение.
Запишем уравнение искомой прямой в
отрезках
![]() нужно
найти a
и b.
нужно
найти a
и b.
Так
как прямая проходит через точку![]() , то ее координаты удовлетворяют уравнению
этой прямой:
, то ее координаты удовлетворяют уравнению
этой прямой:
![]() или
или
![]()
Площадь
треугольника, отсекаемого от координатного
угла, равна
![]() или
или
![]() .
.
Таким образом, нужно решить две системы уравнений:
![]()
Решая
первую систему
![]() ,
получим
,
получим![]()
Решая
вторую систему![]()
Получим
![]()
![]()
![]()
Условию задачи удовлетворяют три прямые:
![]()
![]()
![]()
18. Каноническое уравнение прямой на плоскости.
Пусть
М1(x1, y1, z1) – точка, лежащая на прямой l, и
![]() – её направляющий вектор. Вновь возьмём
на прямой произвольную точку М(x,y,z) и
рассмотрим вектор
– её направляющий вектор. Вновь возьмём
на прямой произвольную точку М(x,y,z) и
рассмотрим вектор![]()
 Ясно,
что векторы
Ясно,
что векторы
![]() и
и![]() коллинеарные, поэтому их соответствующие
координаты должны быть пропорциональны,
следовательно,
коллинеарные, поэтому их соответствующие
координаты должны быть пропорциональны,
следовательно,
![]() – канонические уравнения прямой.
– канонические уравнения прямой.
Замечание
1. Заметим, что канонические уравнения
прямой можно было получить из
параметрических,исключив параметр t.
Действительно, из параметрических
уравнений получаем![]() или
. Пример. Записать уравнение прямой
или
. Пример. Записать уравнение прямой
![]() в параметрическом виде. Обозначим
в параметрическом виде. Обозначим![]() , отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.
, отсюда x = 2 + 3t, y = –1 + 2t, z = 1 –t.
Замечание
2. Пусть прямая перпендикулярна одной
из координатных осей, например оси Ox.
Тогда направляющий вектор прямой
перпендикулярен Ox, следовательно, m=0.
Следовательно, параметрические уравнения
прямой примут вид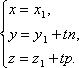 Исключая
из уравнений параметр t, получим уравнения
прямой в виде
Исключая
из уравнений параметр t, получим уравнения
прямой в виде
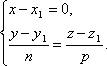 Однако
и в этом случае условимся формально
записывать канонические уравнения
прямой в виде
Однако
и в этом случае условимся формально
записывать канонические уравнения
прямой в виде![]() .
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает,
что прямая перпендикулярна соответствующей
координатной оси. Аналогично, каноническим
уравнениям
.
Таким образом, еслив знаменателе одной
из дробей стоит нуль, то это означает,
что прямая перпендикулярна соответствующей
координатной оси. Аналогично, каноническим
уравнениям
![]()
соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz.
Примеры.
Составить канонические и параметрические
уравнения прямой, проходящей через
точку М1(1;0;-2) параллельно вектору![]() . Канонические уравнения:
. Канонические уравнения:![]()
Параметрические
уравнения: