34. Суть тенденції розвитку, методи виявлення та аналізу.

Тенденція (тренд) являє собою напрям розвитку певного соціально-економічного явища. В деяких випадках тенденцію можна встановити за значеннями рівнів ряду динаміки. Наприклад, якщо рівні постійно збільшуються, чи зменшуються. Основні тенденції – зростання чи зниження – можна поділити за їх характером.

Характер основної тенденції можна також встановити за допомогою абсолютних ланцюгових приростів. Якщо абсолютні ланцюгові прирости мають додатні значення, динамічний ряд має тенденцію до зростання. Якщо абсолютні ланцюгові прирости мають від’ємні значення, динамічний ряд має тенденцію до зниження. Якщо абсолютні ланцюгові прирости мають однакові значення, то характер тенденції рівномірний (рівномірне зростання чи рівномірне зниження). Якщо кожен наступний ланцюговий приріст більше за попередній, то тенденція має прискорений характер. Якщо кожен наступний ланцюговий приріст менше за попередній, то тенденція має уповільнений характер.

До найбільш простих методів згладжування динамічних рядів належать методи ступінчастої середньої та плинної середньої. Метод ступінчастої середньої (укрупнення інтервалів) полягає в тому, що рівні первинного динамічного ряду поєднуються в збільшені інтервали і розраховуються середні в кожному зі створених інтервалів.

Суть методу середньої плинної полягає в тому, що середні обчислюються також за збільшеними інтервалами, але на відміну від попереднього методу здійснюється послідовне пересування меж збільшених інтервалів на один первинний інтервал до кінця динамічного ряду.

Якщо значення рівнів похідного (згладженого) динамічного ряду не дають можливості встановити чітку тенденцію, проводять нове згладжування, при цьому беруть ще більші інтервали. Слід зауважити, що для об’єднання беруться інтервали первинного динамічного ряду. Згладжування повторюють доти, доки не виявиться чітка тенденція, або коли не залишиться три укрупнених інтервали, оскільки подальше згладжування вже не має сенсу. Через дві точки завжди можна провести лінію, але при цьому можна отримати результат, протилежний реальному стану.

Якщо згладжування ряду динаміки не дає можливості виявити тенденцію розвитку або її характер, то відповідь на це питання можна напевне одержати за допомогою аналітичного вирівнювання заданого (вихідного) динамічного ряду методом найменших квадратів.

Метод аналітичного вирівнювання дає змогу не лише виявити тенденцію розвитку, а й кількісно виміряти її.

Під аналітичним вирівнюванням ряду динаміки у статистиці розуміють побудову функції Y = f(t), яка аналітично виражає залежність значень ознаки Y від часу t. Такі функції, а також їх графіки називають трендовими кривими. За допомогою трендової кривої завжди можна виявити основну тенденцію розвитку явища, що вивчається, а також її характер.

35. Використання трендових рівнянь при виявленні тенденції розвитку.

Якщо згладжування ряду динаміки не дає можливості виявити тенденцію розвитку або її характер, то відповідь на це питання можна напевне одержати за допомогою аналітичного вирівнювання заданого (вихідного) динамічного ряду методом найменших квадратів.

Метод аналітичного вирівнювання дає змогу не лише виявити тенденцію розвитку, а й кількісно виміряти її.

Під аналітичним вирівнюванням ряду динаміки у статистиці розуміють побудову функції Y = f(t), яка аналітично виражає залежність значень ознаки Y від часу t. Такі функції, а також їх графіки називають трендовими кривими. За допомогою трендової кривої завжди можна виявити основну тенденцію розвитку явища, що вивчається, а також її характер.

Процес побудови трендової кривої складається з двох етапів:

• вибір виду функції f(t)

• обчислення параметрів функції f(t).

На практиці при виборі виду тренду перевага звичайно віддається функціям, параметри яких мають чіткий економічний зміст:

• лінійна – у = a + bt – (a – середній початковий рівень ознаки, b – середній абсолютний приріст)

• квадратична, або параболічна – y = a + bt + ct ² – (a – середній початковий рівень ознаки, b – середня початкова швидкість зростання, с – середній приріст швидкості зростання)

• показникові – y = a·b ^t – (a – середній початковий рівень ознаки, b – середній темп зростання).

Після вибору виду залежності її параметри обчислюються за методом найменших квадратів. Цей метод забезпечує такий вибір параметрів тренду, щоб мінімізувати суму квадратів відхилень фактичних значень рівнів ряду від теоретичних рівнів, що розраховані за відповідних значень t.

Найпростішою формулою, що відтворює тенденцію розвитку, є лінійна функція:

Параметри та згідно методу найменших квадратів знаходяться рішенням системи нормальних рівнянь:

,

де y – фактичні рівні ряду t – порядковий номер періоду або моменту часу.

Розрахунок параметрів значно спрощується, якщо за початок відліку часу (t = 0) обрати центральний інтервал. Значення умовних періодів t залежать від того, парну чи непарну кількість рівнів має динамічний ряд.

Оскільки мета введення умовного нуля – максимальне спрощення розрахунків, то відстані між сусідніми рівнями динамічного ряду з умовними періодами мають бути мінімальними, проте однаковими впродовж усього ряду. Таким чином, у разі парної кількості рівнів динамічного ряду відстані між будь-якими двома рівнями з умовними періодами дорівнюють двом; у разі непарної кількості рівнів динамічного ряду відстані між будь-якими двома рівнями з умовними періодами дорівнюють одиниці. Умовні періоди, розташовані ліворуч умовного нуля, набувають від’ємних значень, а ті, що розташовані праворуч – додатних.

Незалежно від кількості рівнів у динамічному ряді з умовними періодами  t = 0, а тому система нормальних рівнянь для лінійної моделі тренду матиме такий вигляд:

Тоді параметри а₀ та а₁ для лінійної моделі тренду розраховуються за формулами:

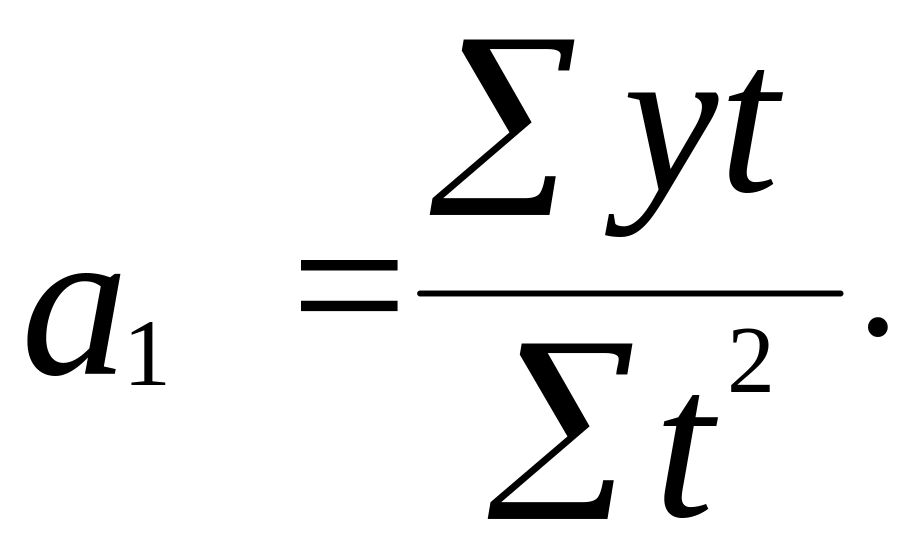(4.9.10)

Якщо у трендовій моделі використовуються нелінійні функції, то вони приводяться до лінійного вигляду за допомогою певних математичних перетворень.