
- •Предмет теории вероятности
- •4.Осн. Правила и формулы комбинаторики
- •6. ГеометрическиОе определение вероятности
- •7. Теоремы сложения вероятностей
- •Свойства функции распределения
- •Свойства математического ожидания
- •20. Нормальное распределение
- •Свойства математического ожидания
- •23. Вероятность попадания нормальной случайной величины в заданный интервал
- •Свойства эмпирической функции распределения
- •33. Точечное оценивание параметров распределения.
- •35. Доверительный интервал и доверительная веротность.
- •36. Доверительные интервалы математического ожидания и для дисперсии нормально распределенной случайной величины.
20. Нормальное распределение
ОПР: Нормальным называется такое распределение случайной величины , плотность вероятности которого описывается функцией Гаусса:
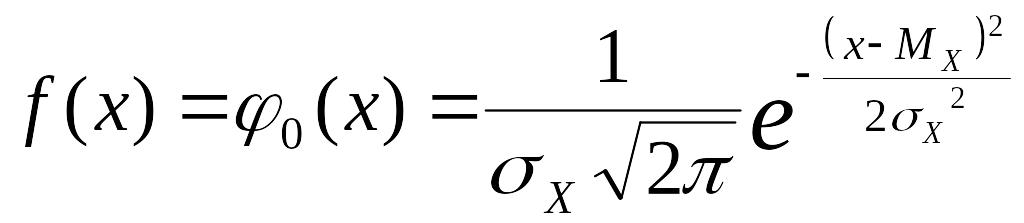
где
![]() – среднее квадратичное отклонение;
– среднее квадратичное отклонение;
![]() – математическое ожидание случайной
величины.
– математическое ожидание случайной
величины.
ТЕОРЕМА: М(х)=m D(x)=ϭ ϭ(x)=ϭ
21. ОПР: Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
,
где .
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно этой величине.
2. M(CX)= C·M(X)
3. M(X+Y)=M(X)+M(Y)
4.
5.
22. ОПР: Дисперсией случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания:
.
свойства дисперсии
Дисперсия постоянной величины равна нулю.
D(X-Y)= D(X)-D(Y)
23. Вероятность попадания нормальной случайной величины в заданный интервал
Во многих практических задачах требуется определить вероятность попадания случайной величины в заданный интервал. Эта вероятность может быть выражена в виде разности функции распределения вероятности в граничных точках этого интервала:
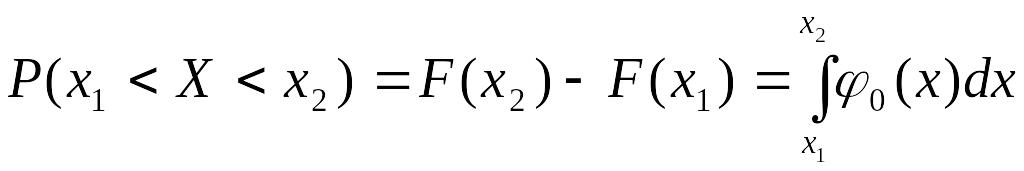 .
.
В случае нормального распределения:

Следовательно, искомая вероятность может быть выражена через веденный ранее стандартный интеграл Лапласа:
 .
.
Функция
Лапласа не выражается через элементарные
функции
 .
.
Для ее вычисления используются специальные таблицы или методы приближенного вычисления.
24. НЕРАВЕНСТВО ЧЕБЫШЕВА
теорема. каково бы ни было ε›0 для любой случ величины х, Д кот конечна имеет равенство Чебышева


25. закон больших чисел
Под законом больших чисел понимают общий принцип в силу кот-й совмест. дейст-е случ факторов приводит при опр-х условиях к результату почти зависящих от испытаний . этот принцип выражается рядом теорем.
В основе доказательств
этих теорем лежит неравенство Чебышева.
Это неравенство можно получить,
рассматривая дискретную случайную
величину, имеющую
возможных значений
![]() .
.
27. ПРЕДМЕТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Математическая стат-ка – раздел матем-ки, в кот изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случ явлений для выявления существующих закономерностей.
Первая задача математической статистики – указать способы сбора и группировки статистических данных, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Второй задачей математической статистики является разработка методов анализа статистических данных в зависимости от целей исследования. К этой задаче относятся: оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и т.п.
Третья задача - проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
28. ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВ-ТИ
Выборочной совокупностью или случайной выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
При составлении выборки можно поступать двумя способами: после того как объект отобран и исследован, его можно возвратить или не возвращать в генеральную совокупность. В связи с этим выборки подразделяются на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. При бесповторной выборке отобранный объект в генеральную совокупность не возвращается.
29. СТАТИС-ОЕ РАСПРЕДЕЛЕНИЕ ВЫБОРКИ.
Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:
X |
|
|
….. |
|
w |
|
|
…. |
|
где относительные
частоты
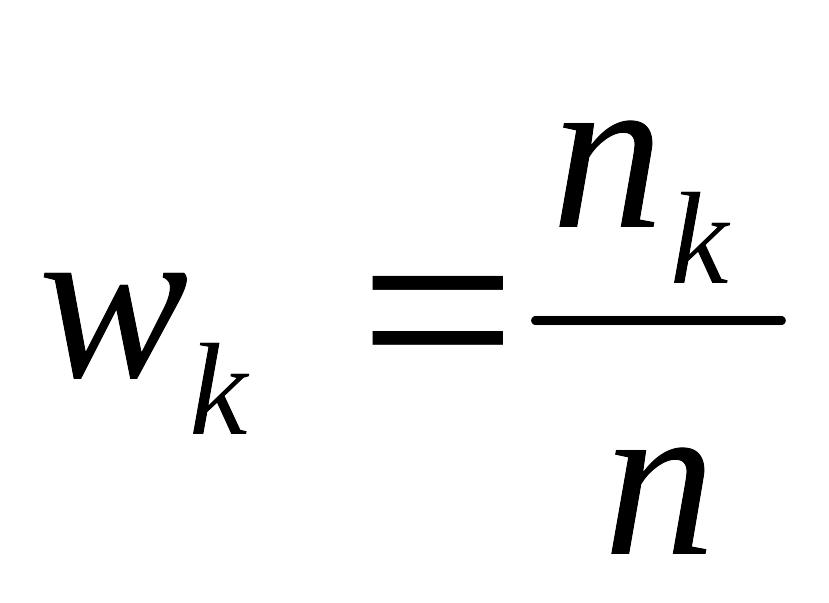 .
.
Приведенный способ
представления статистических данных
применяют в случае дискретных случайных
величин. Для непрерывных случайных
величин удобнее разбить отрезок [a,b]
возможных значений случайной величины
на частичные полуинтервалы
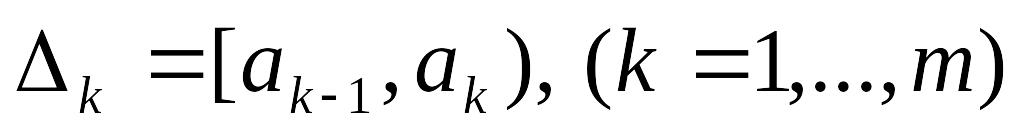 (
( замкнут также и справа) с помощью
некоторой системы точек
замкнут также и справа) с помощью
некоторой системы точек
![]() .
Часто разбиение [a,b]
производят на равные части, тогда:
.
Часто разбиение [a,b]
производят на равные части, тогда:
![]()
где
 .
.
30.ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ.
Эмпирической
функцией распределения
(функцией распределения выборки) называют
функцию
![]() ,
определяющую для каждого значения x
относительную частоту события X<x.
Таким образом, по определению
,
определяющую для каждого значения x
относительную частоту события X<x.
Таким образом, по определению
![]() ,
где
,
где
![]() – число вариант, меньших x,
n
– объем выборки.
– число вариант, меньших x,
n
– объем выборки.
