7. Теоремы сложения вероятностей

Теорема: Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:

.

Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

.

8. Теоремы умножения вероятностей

Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

.

Теорема: Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий:

Р(А₁·А₂·…·А_n)= Р(А₁)·(А₂)·…·Р(А_n)

Теорема: вер-ть совм-го появл-я 2-х незав-х соб-й А и В равна произв-ю вер-ти этих соб-й

Р(АВ)= Р(А)·Р(В)

Теорема: Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий:

.

26.ТЕОРЕМА БЕРНУЛЛИ

вероятность того, что событие наступит в любых испытаниях, определяется по формуле Бернулли:

.

опр:Число наступлений события называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления любое другое количество раз.

Теорема. Наивероятнейшее число наступлений события в независимых испытаниях заключено между числами _≤k≤

9.ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.

Предположим, что событие может произойти только с одним из несовместных событий . Например, в магазин поступает одна и та же продукция от трех предприятий и в разном количестве. Вероятность выпуска некачественной продукции на этих предприятиях различна. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие ). Здесь события – это выбор изделия из продукции соответствующего предприятия.

В этом случае вероятность события можно рассматривать как сумму произведений событий .

По теореме сложения вероятностей несовместных событий получаем . Используя теорему умножения вероятностей, находим:

.

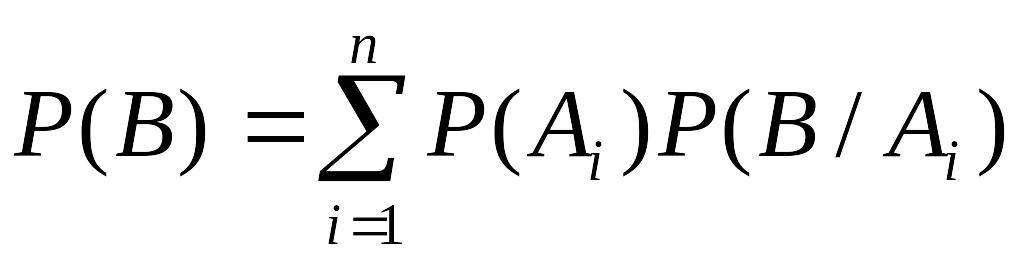Полученная формула называется формулой полной вероятности.

10. ФОРМУЛА БАЙЕСА

На основании теоремы о вероятности произведения двух событий:

,

откуда:

или

.

Полученная формула носит название формулы Байеса

11. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ. ФОРМУЛА БЕРНУЛИ

Серия повторных независимых испытаний, в каждом из которых данное событие имеет одну и ту же вероятность , не зависящую от номера испытания, называется схемой Бернулли. Таким образом, в схеме Бернулли для каждого испытания имеются только два исхода: событие (успех), вероятность которого и событие (неудача), вероятность которого .

Рассмотрим задачу: в условиях схемы Бернулли необходимо определить вероятность того, что при проведении независимых испытаний, в испытаниях наступит событие , если вероятность его наступления в каждом испытании равна .

Определим вначале вероятность того, что в первых испытаниях событие наступит, а в остальных испытаниях не наступит. Вероятность такого события можно получить по формуле вероятности произведения независимых событий , где .

Это лишь одна из возможных комбинаций, когда событие произошло только в первых испытаниях. Для определения искомой вероятности нужно перебрать все возможные комбинации. Их число равно числу сочетаний из элементов по , т.е. .

Таким образом, вероятность того, что событие наступит в любых испытаниях, определяется по формуле Бернулли:

.

12. ЛОКАЛЬНАЯ ФОРМУЛА МУАВРА-ЛАПЛАСА

, где , а – функция Гаусса, для кот имеются таблицы.

13. ИНТЕГРАЛЬНАЯ ФОРМУЛА МУАВРА-ЛАПЛАСА.

,

где , .

14. СЛУЧАЙНАЯ ВЕЛИЧИНА.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.

Случайная величина обычно обозначается прописной латинской буквой ( ), ее конкретные значения – строчными буквами ( ).

Случайной величиной называется функция , определенная на множестве элементарных событий , .

Случайные величины делятся на дискретные и непрерывные.

Величина называется дискретной, если она может принимать определенные, фиксированные значения.

Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга.

15. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕЕ СВ-ВА