
- •Предмет теории вероятности
- •4.Осн. Правила и формулы комбинаторики
- •6. ГеометрическиОе определение вероятности
- •7. Теоремы сложения вероятностей
- •Свойства функции распределения
- •Свойства математического ожидания
- •20. Нормальное распределение
- •Свойства математического ожидания
- •23. Вероятность попадания нормальной случайной величины в заданный интервал
- •Свойства эмпирической функции распределения
- •33. Точечное оценивание параметров распределения.
- •35. Доверительный интервал и доверительная веротность.
- •36. Доверительные интервалы математического ожидания и для дисперсии нормально распределенной случайной величины.
Предмет теории вероятности
Теория вероятностей – математическая дисциплина, изучающая закономерности в случайных явлениях.
Случайным в теории вероятностей называют событие, которое при данном испытании, в данном опыте может либо произойти, либо не произойти и для которого имеется определенная вероятность его наступления.
опр: экспериментом или опытом наз осущ-е намеч-го дейст-я и получение его рез-та. предметом ТВ, кот изучает закономерности случ явлений явл модели экспер-в со случ исходами. элем соб-ем наз каждый из равнов-х рез-в испытаний. всякий мыслимый рез экспет-та наз элем соб-ем и оброзн ω1, ω2,…, ωn.
простр-вом элем
соб-й наз мн-во всех взаимно исключающих
экспер-та. обозн.
![]()
Математическая модель случайного эксперимента включает в себя:
1) построение
множества элементарных исходов
![]() ;
;
2) описание множества событий для данного эксперимента;
3) задание вероятностного распределения на множестве событий.
2. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ КЛАССИФИКАЦИЯ
Из элементарных исходов можно составить более сложное событие. Результат испытания называется событием, независимо от его значимости. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием.
опр:Каждое случайное
событие
![]() определяется как подмножество в множестве
элементарных событий
.
При этом те элементарные события из
,
при которых событие
наступает (т.е. принадлежит подмножеству
)
называют благоприятствующими
событию
.
определяется как подмножество в множестве
элементарных событий
.
При этом те элементарные события из
,
при которых событие
наступает (т.е. принадлежит подмножеству
)
называют благоприятствующими
событию
.
опр:Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого. Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны.
Другими словами,
события
и
![]() совместны, если соответствующие множества
и
имеют общие элементы, и несовместны в
противном случае, если появление одного
из них исключает появление другого, и
соответствующие множества
и
не имеют общих элементов.
совместны, если соответствующие множества
и
имеют общие элементы, и несовместны в
противном случае, если появление одного
из них исключает появление другого, и
соответствующие множества
и
не имеют общих элементов.
опр: Достоверным
называют событие, которое обязательно
произойдет, если будет осуществлена
определенная совокупность условий
![]() .
Невозможным
называют событие, которое заведомо не
произойдет, если будет осуществлена
определенная совокупность условий
.
.
Невозможным
называют событие, которое заведомо не
произойдет, если будет осуществлена
определенная совокупность условий
.
Событие, совпадающее
с пустым множеством
![]() ,
называется невозможным
событием, а событие, совпадающее со всем
множеством
,
называется достоверным
событием.
,
называется невозможным
событием, а событие, совпадающее со всем
множеством
,
называется достоверным
событием.
опр: События называют равновозможными, если нет основания полагать, что одно событие является более возможным, чем другие.
3.ДЕЙСТВИЯ НАД СОБЫТИЯМИ
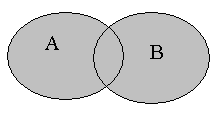
![]() (
(![]() )
–
сумма событий.
Это событие, состоящее в том, что произошло
хотя бы одно из двух событий
)
–
сумма событий.
Это событие, состоящее в том, что произошло
хотя бы одно из двух событий
![]() или
или
![]() (не исключающее логическое «или»).
(не исключающее логическое «или»).
(
 )
–
произведение
событий.
Это событие, состоящее в совместном
осуществлении событий
и
(логическое «и»).
)
–
произведение
событий.
Это событие, состоящее в совместном
осуществлении событий
и
(логическое «и»).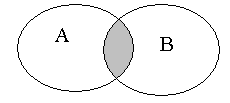
3.
![]() (множество элементов, принадлежащих
,
но не принадлежащих
)
– разность
событий.
(множество элементов, принадлежащих
,
но не принадлежащих
)
– разность
событий.

4. Противоположным
(дополнительным)
для события
(обозначается
![]() )
называется событие, состоящее из всех
исходов, которые не входят в
.
)
называется событие, состоящее из всех
исходов, которые не входят в
.

![]()
Два события называются противоположными, если появление одного из них равносильно непоявлению другого.
