Электромеханические аналогии уравнения Лагранжа-Максвелла

Электромеханическая система обладает не только механической, но и электрической (электромагнитной) энергией, сосредоточенной в элементах ее электрической цепи (индуктивностях, конденсаторах и резисторах).

Поскольку процессы в электрических цепях описываются также дифференциальными уравнениями, существуют определенные аналогии между механическими и электрическими величинами, описывающими поведение системы.

Первая система аналогий между механическими и электрическими цепями более "физична", поэтому в основном 6удем пользоваться ею, хотя в некоторых случаях применение второй системы дает более простые уравнения.

Из этой системы видно, что ЭДС в электрической цепи аналогична силе, индуктивность аналогична массе и обладает инерционностью, и энергия, запасаемая в магнитном поле, является кинетической энергией. Конденсатор, аналогично пружине, запасает энергию, которую логично считать потенциальной. Активное сопротивление действует аналогично механическому вязкому сопротивлению, и энергия, выделяемая на нем, рассеивается в виде тепла.

Тогда простейшей механической цепи, содержащей массу, пружину и вязкое сопротивление, и описываемой уравнением вида

можно поставить в соответствие простейшую электрическую цепь с последовательно включенными индуктивностью, емкостью и сопротивлением, описываемую уравнением

где L·q``- ЭДС самоиндукции, R·q`- падение напряжения на сопротивлении, S·q- напряжение на емкости.

Электромеханическую систему, имеющую S_m степеней механической свободы и S₁ независимых электрических контуров, учитывая электромеханические аналогии, можно представить в виде механической системы, имеющей S_m+S₁ степеней свободы и обладающей:

суммарной электромеханической кинетической энергией T_Σ=T_M+W_M;

потенциальной энергией П_Σ=П_М+W_Э;

мощностью рассеяния D_Σ=D_M+D_Э.

Отсюда движение в такой системе будет описываться уравнениями, аналогичными уравнениям Лагранжа и называемыми уравнениями Лагранжа-Максвелла :

,

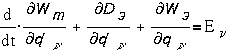
Первые S_m уравнений описывают механические движения в системе (механические уравнения), последующие S₁ уравнений описывают процессы в электрических цепях (электрические уравнения - уравнения 2-го закона Кирхгофа).

26. Затухающие и вынужденные электромагнитные колебания.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:

, (7.1.1)

г де - коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Например, для пружинного маятника где r - коэффициент сопротивления, т.е. коэффициент пропорциональности между скоростью и силой сопротивления. Для затухающих колебаний в колебательном контуре , где R - величина активного сопротивления контура.

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω₀.

Если свободные колебания происходят на частоте ω₀, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.

После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.

В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω₀. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.

Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила F приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону

y = ym cos ωt.

где y_m – амплитуда колебаний, ω – круговая частота.

Такой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение.

Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно:

Δl = x – y = x – ym cos ωt.

Второй закон Ньютона для тела массой m принимает вид :

ma = –k(x – y) = –kx + kym cos ωt.

В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.

Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: Тогда уравнение вынужденных колебаний запишется в виде

(**)

где – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением: