Вступ

Методичні вказівки до практичних занять з курсу „Вища математика” можуть бути використані викладачами і студентами на практичних заняттях з вищої математики у першому навчальному семестрі. Вони містять перелік теоретичних питань, а також типових завдань, які повністю відповідають робочій програмі курсу. Методичні вказівки розбиті на 14 частин, кожна з яких відповідає одному практичному заняттю і містить блок теоретичних питань, завдання для аудиторної роботи, завдання для самостійної роботи, додаткові завдання і відповіді.

Наявність завдань для самостійної роботи з відповідями, а також чіткий перелік теоретичних питань, необхідних для якісної підготовки до наступного заняття, стимулюють самостійну роботу вдома і активну роботу в аудиторії.

Бажаємо успіхів у навчанні!

Заняття № 1.

Матриці. Визначник матриці.

Питання для обговорення.

1. Матриці і дії над ними.

2. Визначник матриці та його властивості.

3. Обернена матриця.

Завдання для аудиторної роботи.

1. Для матриць , і знайти:

а) ; б) ; в) .

2. Для матриць , знайти:

а) ; б) .

3. Для матриць і знайти:

а) ; б) .

4. Обчислити наступні визначники:

а) , б) .

5. Знайти обернені матриці. Зробити перевірку

а) , б) .

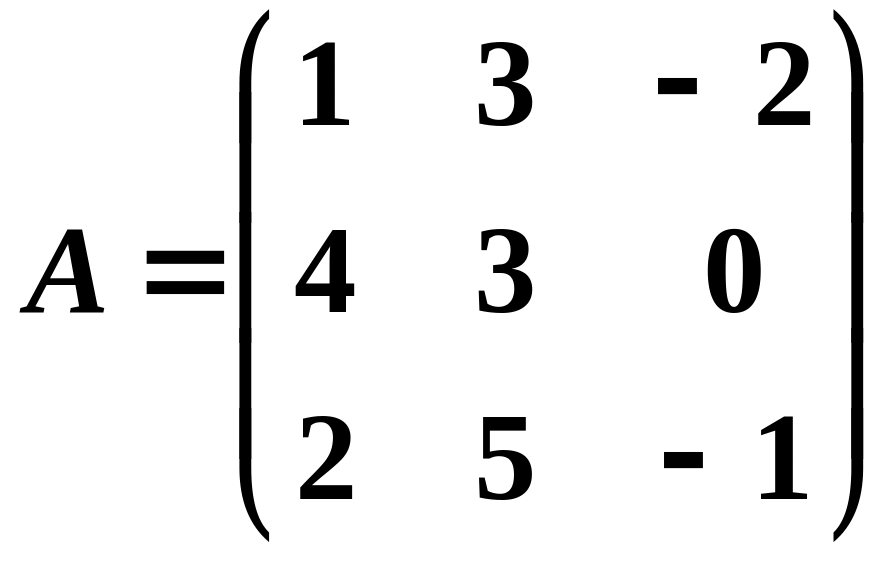Завдання для самостійної роботи.

6. Для матриць 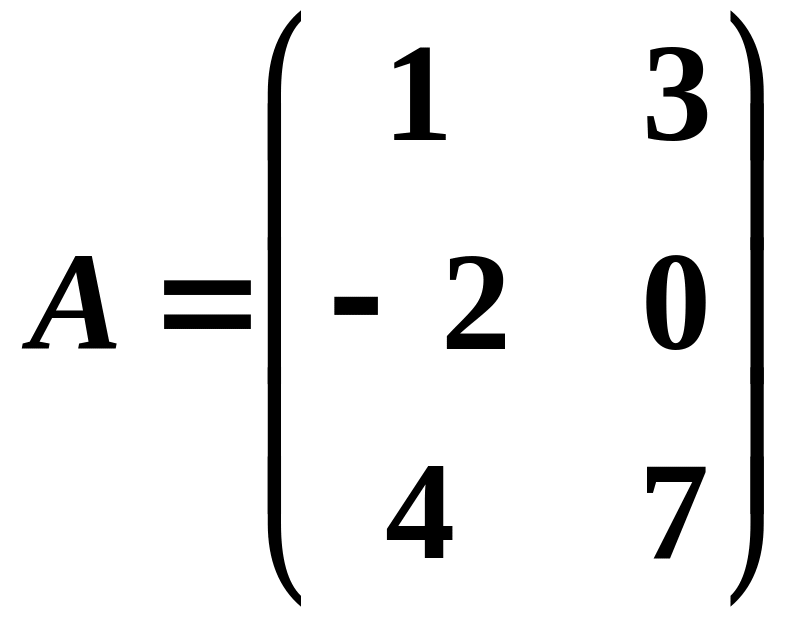, , 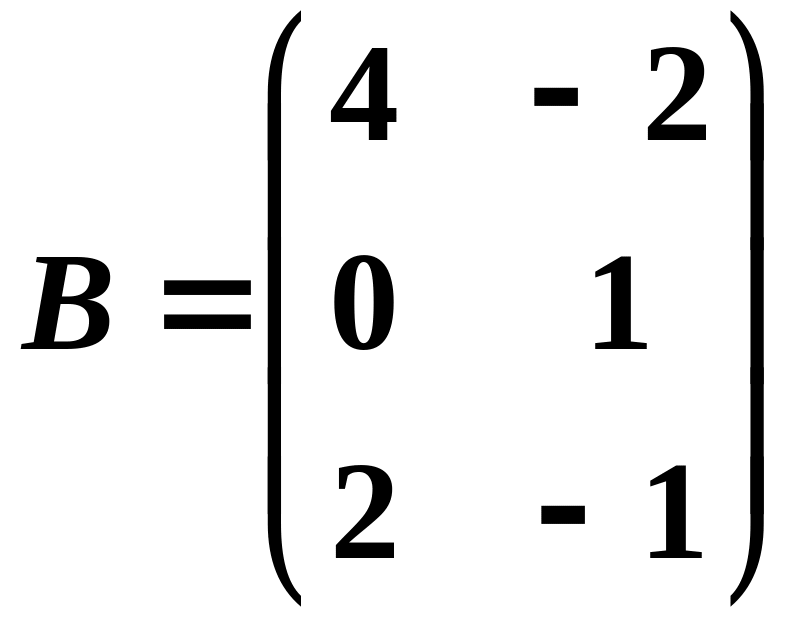знайти:

а) ; б) ; в) .

7. Для матриць і знайти:

а) ; б) .

8. Обчислити визначники

а) , б) .

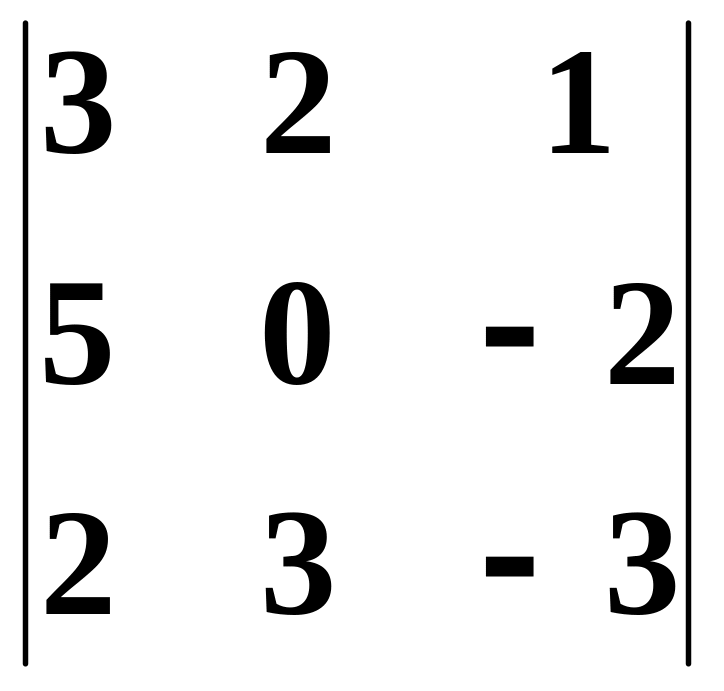9. Знайти обернені матриці. Зробити перевірку

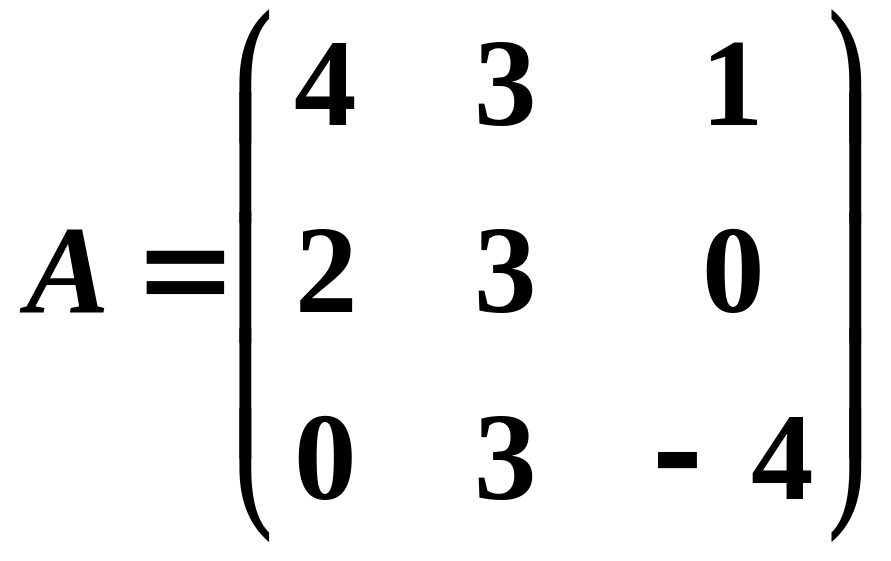а) ; б) ; в) .

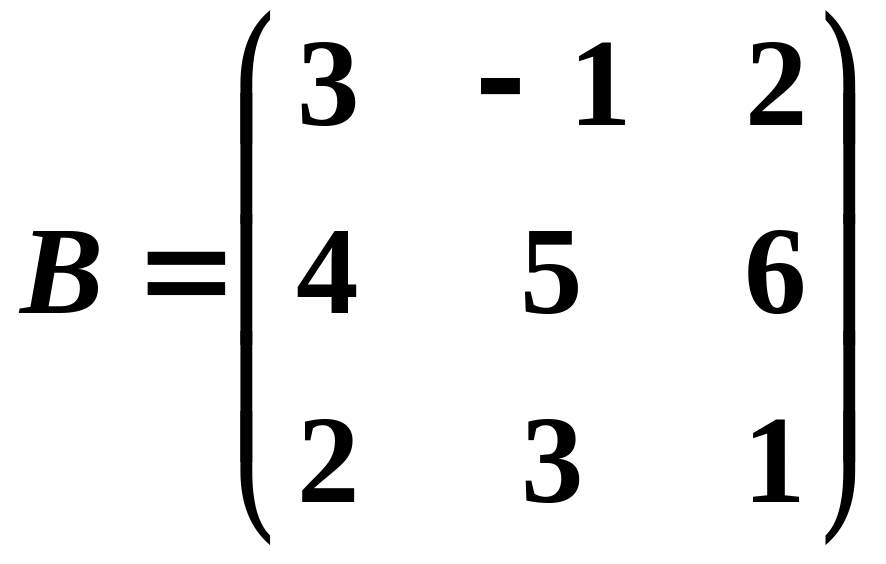Додаткові завдання

10. Обчислити наступні визначники:

а) ; б) .

Розв’язати матричні рівняння

11.

12.

Відповіді

1.1. а) , б) , в) ;

1.2. а) , б) ;

1.3. а) , б) не існує;

1.4. а) -11; б) 44;

1.5. а) , б) ;

1.6. а) , б) , в) ;

1.7. а) 12; б) ;

1.8. а) 2, б) 55;

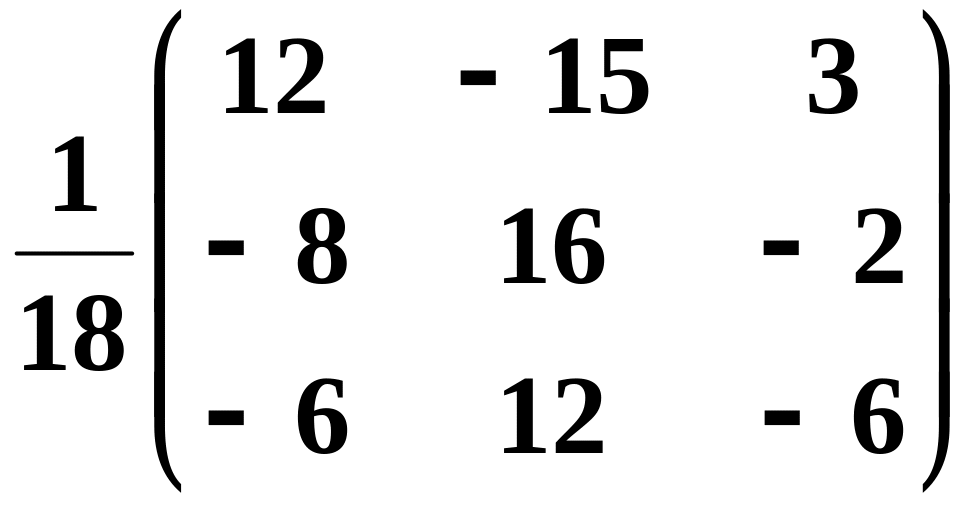1.9. а) , б) , в) ;

1.10. а) -114 б) -95;

1.11. ; 1.12. .

Заняття № 2

Розв’язування систем лінійних рівнянь

Питання для обговорення

1. Правило Крамера.

2. Метод оберненої матриці.

3. Метод Жордана-Гауса.

4. Порівняльний аналіз цих трьох методів.

Завдання для аудиторної роботи

Розв’язати систему кожним з трьох методів.

1. ; 2. .

Завдання для самостійної роботи

Розв’язати систему за допомогою правила Крамера, методом матричного обчислення, методом Жордана-Гауса.

3. ; 4. ;

5. ; 6. .

Відповіді

2.1. ; 2.2. ; 2.3. ; 2.4. ; 2.5. ;

2.6. .

Заняття № 3

Вектори. Лінійна залежність векторів

Базис системи векторів

Питання для обговорення

1. Ранг матриці, його знаходження.

2. Лінійно залежні і лінійно незалежні вектори.

3. Базис системи векторів.

4. Простір 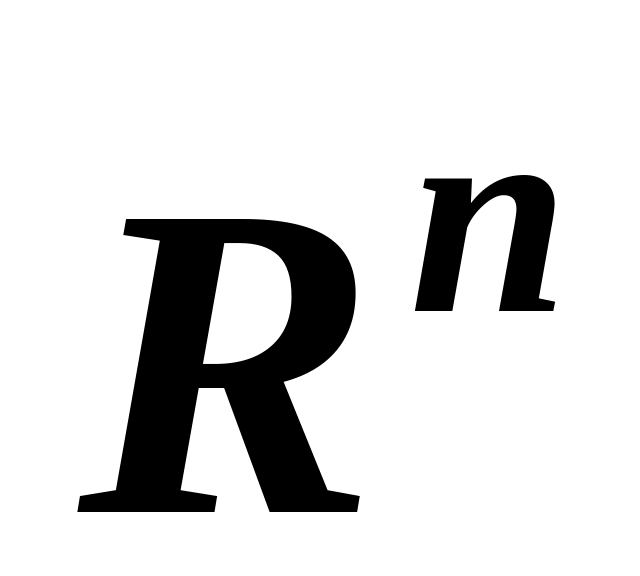. Базис простору .

Завдання для аудиторної роботи

За допомогою метода Жордана-Гауса знайти загальний розв’язок системи лінійних алгебраїчних рівнянь. Записати два частинних розв’язки та базисний розв’язок.

1. ; 2. ;

3. .

Знайти ранг матриці

4. 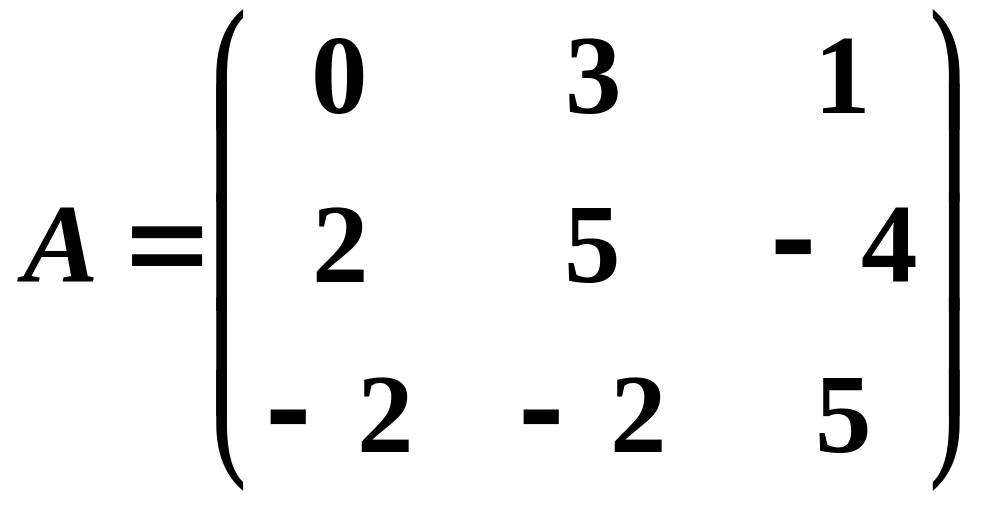; 5. .

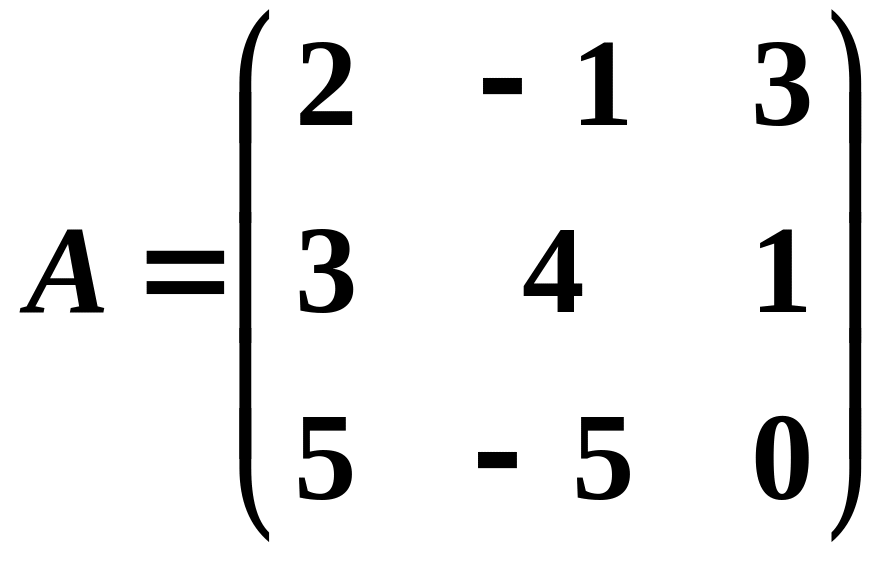6. Для системи векторів визначити ранг і якийсь з базисів та розкласти вектори системи за знайденим базисом.

а) , , , .

б) , , , .

Завдання для самостійної роботи.

За допомогою метода Жордана-Гауса знайти загальний розв’язок системи лінійних алгебраїчних рівнянь. Записати два частинних розв’язки та базисний розв’язок.

7. ; 8. ;

9. .

Знайти ранг матриці

10. ; 11. .

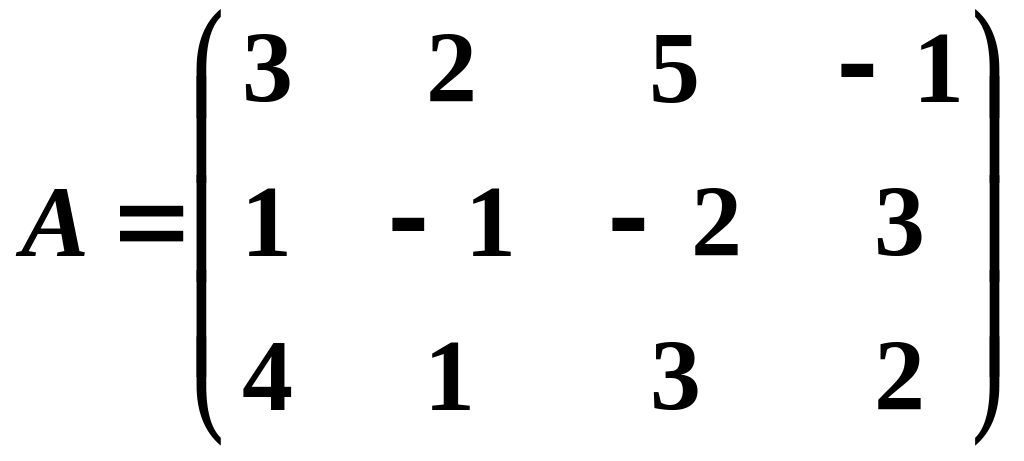12. Для системи векторів визначити ранг і якийсь з базисів та розкласти вектори системи за знайденим базисом.

а) , , , ;

б) , , , ;

в) , , .

Додаткові завдання

Перевірити, чи утворюють вектори базис відповідного простору :

13. , ; 14. , ;

15. , , .

Відповіді

3.1. , , , – вільна змінна;

3.2. система несумісна;

3.3. , , , – вільні змінні;

3.4. 2; 3.5. 3; 3.6. а) , , , ; б) , , , ; 3.7. система несумісна;

3.8. , , , – вільна змінна;

3.9. , , , – вільні змінні; 3.10. 3;

3.11. 2; 3.12. а) , , , ; б) , , , ; в) , , ; 3.13. утворюють; 3.14. не утворюють;

3.15. утворюють.

Заняття №4

Факультативне заняття

1. Два підприємства виготовляють три види продукції. Обсяги (в тис. штук) реалізації за квітень і травень задані матрицями і , де , – елементи матриць, – номер підприємства, – номер виду продукції. По кожному підприємству для кожного вида продукції знайти: а) приріст обсягу реалізації за місяць, б) середньомісячний обсяг реалізації продукції.

2. Підприємство виготовляє два види продукції, використовуючи два типи ресурсів. Норми затрат визначаються матрицею , елементи якої показують, скільки одиниць -го типу ресурсів витрачається на виготовлення одиниці -го виду продукції. Запаси ресурсів задані матрицею-стовпцем . Знайти план випуску продукції за умови повного використання ресурсів.

3. Підприємство виготовляє два види продукції, використовуючи три типи ресурсів. Норми витрат визначаються матрицею , де елементи показують, скільки одиниць -го типу ресурсів витрачається на виготовлення одиниці -го виду продукції. Необхідно знайти: а) собівартість виготовлення одиниці продукції кожного виду, якщо ціни за одиницю ресурсу кожного типа задані матрицею-рядком ; б) витрати ресурсів кожного типу для забезпечення плану випуску продукції, заданої матрицею-рядком ; в) собівартість виконання плану випуску .

Відповіді

1а) ; 1б) ; 2). ; 3а). ; 3б) 3в). 485.

Заняття №5

Пряма на площинi

Питання для обговорення

1. Рівняння прямої на площині.

2. Кут між прямими, умови паралельності та перпендикулярності прямих.

3. Відстань від точки до прямої.

Завдання для аудиторної роботи

1. Задані вершини трикутника 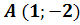, . Знайти:

а) довжини сторін трикутника;

б) рівняння сторін трикутника;

в) внутрішній кут ;

г) рівняння та довжину медіани, проведеної з вершини ;

д) рівняння та довжину висоти, проведеної з вершини ;

е) точку перетину медіани та висоти ;

є) рівняння прямої, яка проходить через точку паралельно .

ж) рівняння та довжину середньої лінії, яка паралельна .