Вопрос 28
Зато есть такая:
– формула интегрирования по частям
собственной персоной. Знаю, знаю, ты
одна такая – с ней мы и будет работать
весь урок (уже легче).
И сразу список в студию. По частям берутся интегралы следующих видов:
1)
,
,
– логарифм, логарифм, умноженный на
какой-нибудь многочлен.
В интегралах
рассматриваемого типа за
всегда обозначается логарифм.
2)
,
– экспоненциальная функция, умноженная
на какой-нибудь многочлен. Сюда же можно
отнести интегралы вроде
–
показательная функция, умноженная на
многочлен, но на практике процентах так
в 97, под интегралом красуется симпатичная
буква «е».
за всегда обозначается многочлен
3)
,
,
– тригонометрические функции, умноженные
на какой-нибудь многочлен.
за всегда обозначается многочлен
4)
,
– обратные тригонометрические функции
(«арки»), «арки», умноженные
на какой-нибудь многочлен.
за всегда обозначается обратная тригонометрическая функция.
Вопрос 29
Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где
.
Затем применяются следующие формулы:
Интеграл
может быть вычислен за k шагов с помощью
формулы редукции
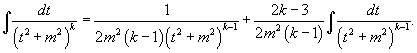
Вопрос 30
Универсальная тригонометрическая подстановка
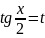
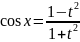
Вопрос 31
1°.Интегралы вида
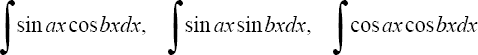
находятся с помощью тригонометрических формул
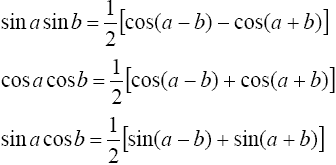
2°. Интегралы вида
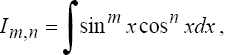
где m и n - четные числа находятся с помощью формул понижения степени
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
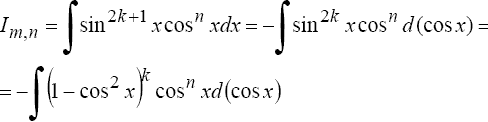
Вопрос 32
Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [a, b] и обозначается следующим образом:
,
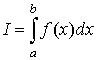или
.
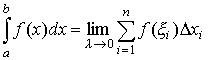В этом случае функция f (x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования. Следует заметить, что не имеет значения, какой буквой обозначена переменная интегрирования определенного интеграла
,
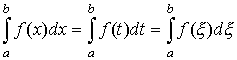поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы. Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы различны: в то время как
представляет семейство функций, определённый интеграл
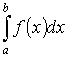
есть число.
Вопрос 33
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если
непрерывна на отрезке
и
— ее любая первообразная на этом отрезке,
то имеет место равенство
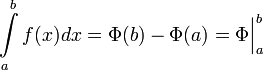
Вопрос 34
В тетради