Вопрос 1

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Функция f (отображение, операция, оператор) — это закон или правило, согласно которому каждому[3] элементу x из множества X ставится в соответствие единственный элемент y из множества Y.[4]

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

Функция является обратной к функции , если выполнены следующие тождества:

f(g(y)) = y для всех

g(f(x)) = x для всех

Вопрос 2

Основные элементарные функции.

К ним относят:

Степенные с целым показателем.

Показательные , где , и .

Логарифмические , где , и .

Тригонометрические

Обратные тригонометрические (аркфункции)

Вопрос 3

Последовательностью называется функция f(n)=x_n, для которой , каждому натуральному числу, ставится в соответствие какое то действительное число.

n - натуральное

x_n – действительное

x_n – энный член последовательности

Часто последовательности задаются при помощи формул и рекуррентно (нет явной формулы для членов последовательности, а члены последовательности с одними номерами выражаются через членов последовательности с другими номерами).

Предел последовательности

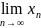
Пределом x_n называется число a, если при Ԑ>0, существует N

n>N→ |x_n-a|< Ԑ

x_n =a+ Ԑ

Вопрос 4

Всякая монотонная ограниченная последовательность имеет предел

Число е:

xⁿ=(1+1/n)ⁿ

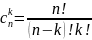
Вопрос 5

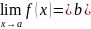
Говорят что предел функции в точке a, если для любого Ԑ, существует δ,из которого |x-a|<δ=>|f(x)- δ|< Ԑ

Для как угодно малого Ԑ найдётся окрестность точки а, в которой значение функции отличается от числа b не больше чем на Ԑ.

Подчеркнём, что в определении предела функции, точка а может не принадлежать области определения функции. Но функция определена в какой-то окрестности точки а.

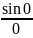– не определено

Вопрос 6

Функция α (x) называется бесконечно малой при , если

Предположим, что α (x) и β (x) - бесконечно малые функции при .

Если 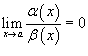, то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);

Если 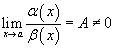, то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;

Если 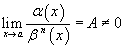, то говорят, что функция α (x) является бесконечно малой порядка n относительно функции β (x);

Если 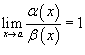, то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при .

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Функция f (x) называется бесконечно большой функцией в точке х = x0 (или x → x0), если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х0 | < δ , выполняется неравенство | f (x) | > К.

В этом случае пишут

и говорят, что функция стремится к бесконечности при х → х0 , или что она имеет бесконечный предел в точке х = х0.

Если f (x) — бесконечно большая функция, то есть бесконечно малая функция в этой же точке.