42. Ядерная модель атома.
Ядерная модель атома приписывала атому строение, аналогичное строению Солнечной системы, в центре которой находится положительно заряженное ядро, вокруг которого, подобно планетам , движутся электроны, удерживаемые у ядра силами кулоновского притяжения.
Действительное строение атома мог выяснить только эксперимент, задача которого состояла в том, чтобы определить распределение электрического заряда в атоме.
Формула Резерфорда.
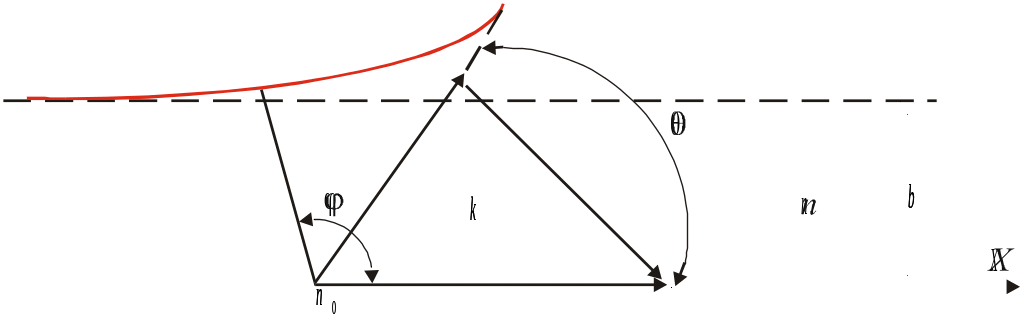
Точечные
заряды взаимодействуют по закону Кулона.
Рассмотрим теорию рассеяния на силовом
кулоновском центре. Рассмотрим движение
частицы с массой
и
зарядом
в кулоновском поле другой частицы с
.
Будем считать, что
,
так, что вторую частицу можно считать
неподвижной. Используя закон сохранения
момента импульса
,
где
-скорость
рассеиваемой частицы на бесконечность,
b-прицельное расстояние, т.е. расстояние
наименьшего сближения частиц, если бы
взаимодействие
между ними
отсутствовало. Точками обозначены
производные по времени.
Введем
новую независимую переменную
и учтем, что
.
Тогда по первой формулы
.
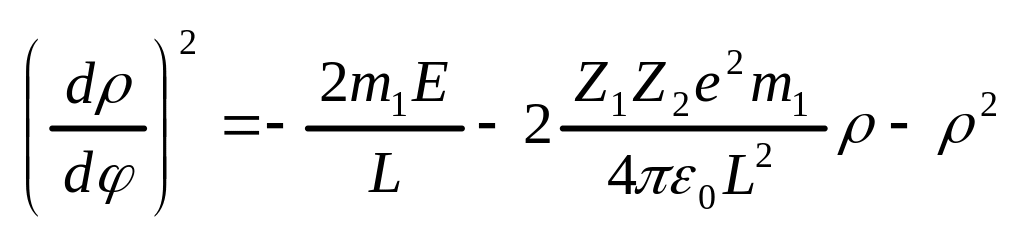Дифференцируя это выражение по
,
получим для определения
уравнение
,
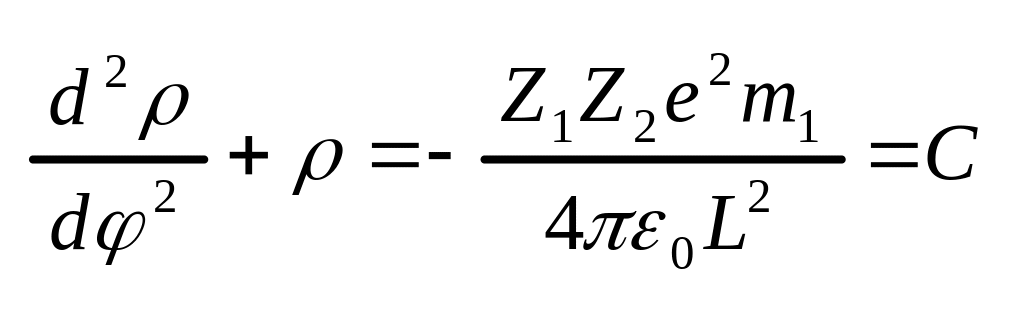общее решение которого
.
При условиях
при
можно найти
,
тогда уравнение примет вид
.
Полагая, что
,
находим угол рассеяния:
.
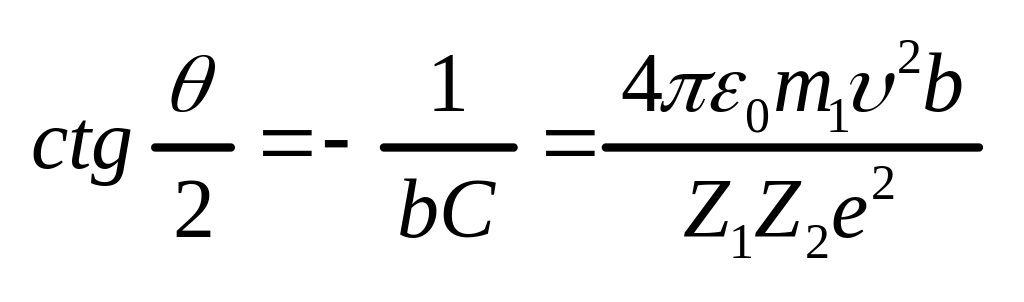Перейдем к статическим характеристикам
рассеяния. Дифференциальное поперечное
сечение
упругого рассеяния в угол между
и
определяется как отношение числа частиц
,
рассеянных в угол между
и
к потоку падающих частиц N:
.
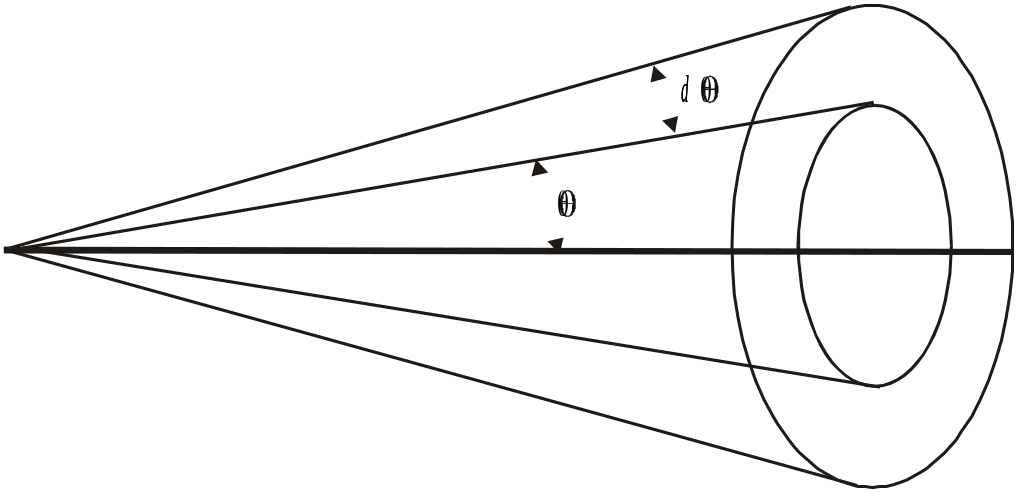
Отсюда следует, что все частицы, прицельные
расстояния которых заключены между b и
b+db, будут рассеяны в угол между
и
.
Число частиц с прицельным расстоянием
между b и b+db равно числу частиц, падающих
на кольцевую площадь радиусом b и шириной
db:
.
Дифференциальное поперечное сечение
.
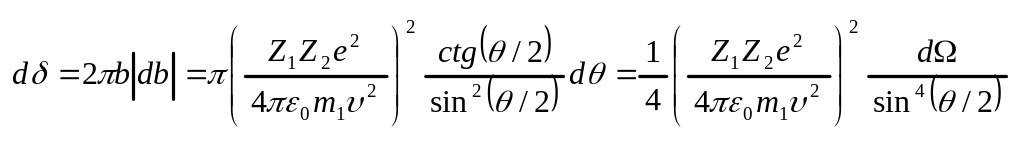Здесь
-
телесный угол между конусами с углами
и
.
Эта формула называется формулой
Резерфорда. С ее помощью Резерфорд
проанализировал результаты своих опытов
по рассеянию
-частиц
на атомах и установил структуру атомов.
Опыты Резерфорда.
Для
своих опытов Резерфорд воспользовался
-частицами,
которые вылетают из атомов радиоактивных
элементов.
-частица
является ядром атома гелия, т.е. несет
с собой положительный заряд 2e и имеет
массу, равную примерно 4-м массам протона.
Поэтому для анализа рассеяния
-частиц
воспользуемся формулой Резерфорда с
.масса
атомов, на которых рассеиваются
-частицы,
предполагается намного больше массы
-частиц.
От
этого ограничения легко освободиться,
если под массой
понимать
массу системы из двух взаимодействующих
частиц. Пучок
-частиц
известной интенсивности направляется
на тонкую мишень, где они рассеиваются
на атомах этой мишени. Число
-частиц,
рассеиваемых на различные углы,
подсчитывается с помощью специальных
счетчиков. Формулой Резерфорда
определяется число частиц, рассеянных
одним рассеивающим центром. Если число
этих центров равно n, то число рассеянных
в телесный угол
частиц равно
,
где Ze – заряд ядра рассеивающего атома.
Если зафиксировать телесный угол
=const,
в котором подсчитываются частицы под
различными углами рассеяния
,
то из последней формулы получаем
.
В эксперименте было проверено соблюдение
последнего условия(формулы). Оказалось,
сто хотя каждый из сомножителей в левой
части равенства изменялся в 1000 раз, их
произведение оставалось постоянным.
Это означает, что формула(предпоследняя)
правильно описывает рассеяние и роль
многократных рассеяний несущественна.
Несовместимость планетарной модели атома с классическими представлениями.
Благодаря наличию центростремительного ускорения у движущихся вокруг ядра электронов они должны непрерывно излучать электромагнитные волны. В результате потери энергии они должны упасть на ядро, т.е. планетарной модели существовать не может. С точки зрения классической физики частота излучения атома должна совпасть с частотой обращения электронов. Такой характер спектра излучения полностью противоречит наблюдаемым закономерностям атомных спектров. С классической точки зрения электрон может описывать вокруг ядра всевозможные орбиты. Идея о дискретном ряде возможных орбит электрона находится в глубоком противоречии с классической планетарной моделью. Революционный шаг по устранению этих противоречий был сделан Бором.