4. Пространственная и временная когерентность. Оценить радиус когерентности солнечного света близи поверхности Земли. Радиус Солнца равен ; среднее расстояние до Земли .

Волны называются когерентными, если они удовлетворяют следующим 3 условиям:

Они имеют одинаковую частоту, т.е. они монохроматичны

Разность фаз , является функцией координаты и не является функцией от времени.

Волновые вектора и параллельны друг другу и направлены перпендикулярно фронту волнны.

Любой не хроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга называется временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т.е. . Прибор обнаружит чёткую интерференционную картину лишь тогда, когда время разрешения прибора значительно меньше времени когерентности накладываемых световых волн.

Если волна распространяется в однородной среде, то фаза колебаний в определ ённой точке пространства сохраняется только в течение время когерентности . За это время волна распространяется в вакууме на расстояние , называемое длиной когерентности. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.

Чем ближе волна к монохроматической, тем меньше ширина спектра её частот и больше время когерентности, а следовательно, и длина когерентности . Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называемая временной когерентностью.

Для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости, перпендикулярной направлению распространения волны, называют пространственной когерентностью.

Радиусом когерентности называется максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции.

Учитывая, что радиус когерентности можно оценить из формулы . Найдём из прямоугольного треугольника .Минимальный радиус когерентности солнца при длине волны равной 480 нм

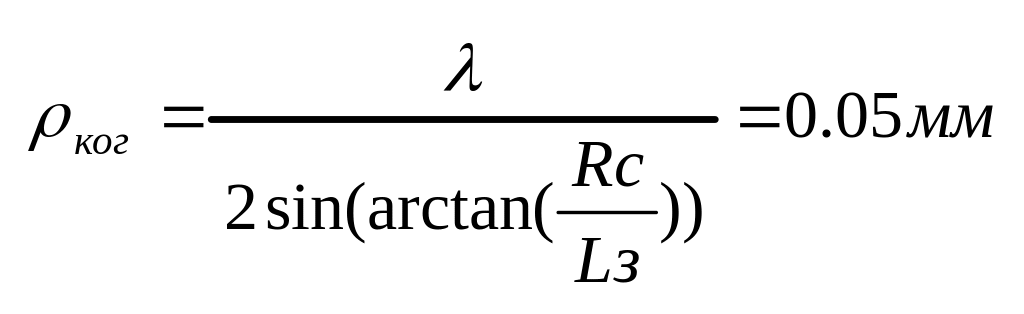
6.Интерференция в тонких пленках.

При падении световой волны на тонкую прозрачную пластину происходит отражение от обеих поверхностей. В результате возникают две световые волны, которые при известных условиях могут интерферировать. Лучи 1 и 2 будут давать интерференцию в отраженном свете, а 1’ и 2’- в походящем. В отраженном свете интенс ивности одинаковы , следовательно интерференция контрастна, а в проходящем свете интерференция размазана, т. к. значительно больше.

Разность хода лучей 1 и 2 до того, как они сойдутся в точке C, равна , где - длина отрезка BC, а - суммарная длина отрезков AO и OC, n- показатель преломления пластинки. Из рис. (b- толщина пластинки). Тогда Произведя замену и учтя, что , получим . В точке С происходит отражение от границы раздела среды, оптически менее плотной, со средой, оптически более плотной. Поэтому фаза волны претерпевает изменение на , т.е. возникает разность фаз, которая учитывается в .

Для того, чтобы имела место временная когерентность, разность хода не должна превышать длину когерентности, равную . Следовательно должно соблюдаться условие или . В полученном соотношении половиной можно пренебречь по сравнению с . Выражение имеет величину порядка единицы, поэтому . Теперь рассмотрим условия соблюдения пространственной когерентности. Расстояние между падающими лучами 1 и 2 равно .

Разность хода зависит от b-толщины пластинки, . При константе угла падения разность хода меняется за счет b и тип полос называется полосы равной толщины. Когда разность хода обуславливается изменением угла падения, то тип полос наз. полосы равного наклона.

Классическим примером полос равной толщины являются кольца Ньютона. Они соблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластины и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении- эллипсов. Найдем радиусы колец при нормальном падении света.

Т. к. , -для светлых, - для темных.

, чем больше m , тем теснее расположены кольца. Для светлых колец . Более точный результат, если брать разность двух колец .