Вопрос 16.Тригонометрическа форма комплексного числа. Показательная форма. Действия над числами, заданными в тригонометрической и показательной формах.

1Тригонометрическая формула комплексного числа. (см. вопрос 15 – комплексная плоскость)

2Действия над числами в тригонометрической и показательной формах

Если даны:

, то:

Аналогично: .

Из формулы произведения получим формулу для степени с натуральным показателем n:

. При r =1 приходим к формуле Муавра:

Пример:

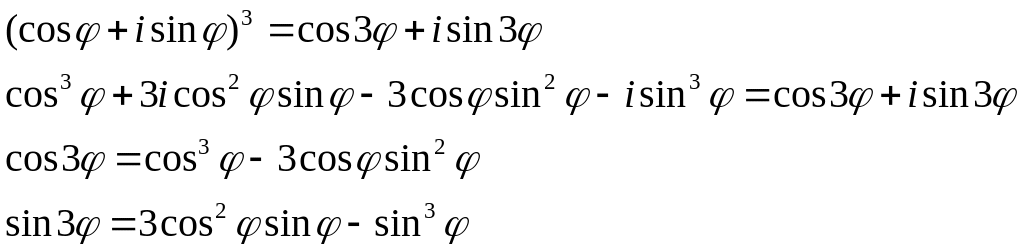
Если n – натуральное число и C – комплексное число, то - решение уравнения

при С 0 существует ровно n различных корней n-степени из C. Они определяются формулами: , где - арифметический корень из положительного числа, - аргумент argC, k=0,1,2,…n-1

Отметим, что

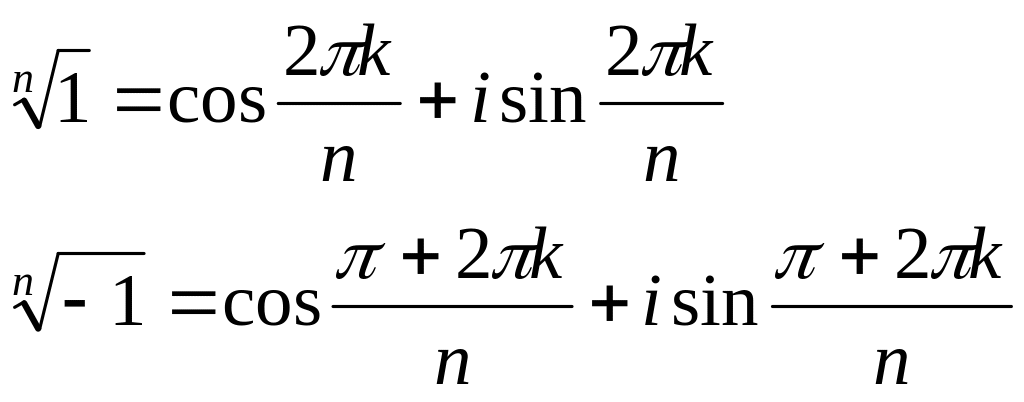
Пусть n=4,

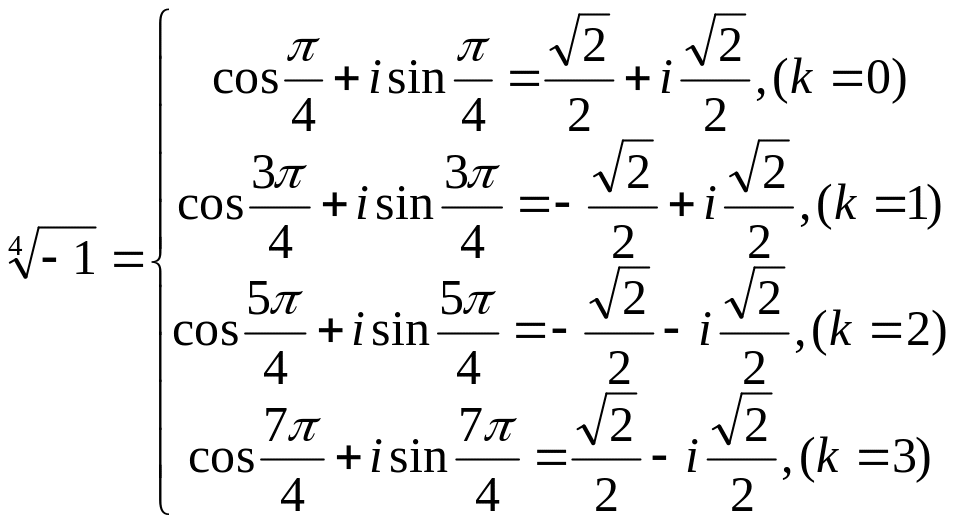
3Показательная форма комплексного числа

С помощью формулы Эйлера - произвольное действительное число, можно перейти от тригонометрической формы числа к показательной:

В частности:

Приведем формулы для степени с натуральным показателем n и для n-ой степени в случае показательной формы комплексного числа: ;

Вопрос17. Извлечение корня из комплексного числа. Решение уравнений вида

(См. вопрос 16)

Вопрос 18.Дифференциальные уравнения (определение, общее и частное решения) Уравнения с разделяющимися переменными, линейные уравнения.

1Определения

Дифференциальным уравнением называется уравнение, в котором искомыми являются функции одной или нескольких переменных, причем уравнения содержат как сами искомые функции, так и их производные или дифференциалы. Порядок старшей из производных или старшего из дифференциалов называется порядком дифференциального уравнения.

Если искомые функции, входящие в дифференциальное уравнение зависят от нескольких аргументов и уравнения содержат частные производные от этих функций по нескольким переменным, то такое уравнение называется уравнением в частных производных.

Если искомая функция зависит от 1 аргумента, то дифференциальное уравнение называется обыкновенным.

Общий вид обыкновенного дифференциального уравнения:

F(x,y,y’,y’’,… )=0

Решением дифференциального уравнения называется любая функция f(x), удовлетворяющая данному дифференциальному уравнению. Основной задачей теории дифференциальных уравнений является отыскание всех решений данного дифференциального уравнения и изучение свойств в этих решениях, причем предварительно нужно доказать, что это решение существует.

Примеры:

1.Проверить, является ли функция y=2x решением дифференциального уравнения xy'-y=0

Решение:

Y’=2 x*2-2x=0; 0=0 =>является решением

2.Для дифференциального уравнения y'y+x показать, что соотношение является его решением.

Решение:

Найдем y' как производную неявной функции 2x+2yy'=0; x+yy’=0

Нахождение решений дифференциальных уравнений называется интегрированием дифференциальных уравнений.

ДУ 1-ого порядка

В общем случае обыкновенное дифференциальное уравнение 1ого порядка записывается так: F(x,y,y’)=0. Пусть дано дифференциальное уравнение 1-ого порядка y'=f(x,y); пусть -решение этого ДУ. Предположим, что функция f(x,y) определена в некоторой области D плоскости XY. Уравнение y'=f(x,y) задает в каждой точке области D значение углового коэффициента касательной к кривой, являющейся графиком функции y= и проходит через эту точку. Тогда задачу отыскания решений ДУ можно сформулировать как залачу отыскания кривой y= ,которая в каждой своей точке имеет указанную уравнением касательную. Естественно, что такая кривая не единственная - это целое семейство кривых.

Линии в области D, имеющие в каждой точке направления, заданные дифференциальным уравнением называются интегральными.

Задача Каши

Как было показано ранее ДУ имеет бесконечное множество решений y= , где с-произвольная постоянная. При этом с входит таким образом, что все решения получаются из y= при различных с. Задача Каши для дифференциального уравнения 1-ого порядка формулируется так: найти такое решение ДУ F(x,y,y’)=0, для которого , где - заданные числа, называемые начальными условиями. С геометрической точки зрения решить задачу Каши значит из всего семейства интегральных кривых выбрать кривую, проходящую через точку ( ), заданную в области D.

Теорема о существовании и единственности решения ДУ

На практике довольно часто пользуются приближенными метолами решения ДУ. Однако, предварительно нужно убедиться в существовании и единственности искомого решения.

Пусть в ДУ y'=f(x,y) функция f(x,y) и ее частная производная определены и непрерывны на открытом множестве D. ( ). Тогда в некоторой области существует непрерывное решение y(x) задачи Каши и при том единственное.

2Общее и частное решения ДУ

Пусть ДУ y'=f(x,y) задано в замкнутой ограниченной области R, в каждой внутренней точке которой задано условие теоремы Каши (о существовании единственности решения). Общим решением ДУ y'=f(x,y) в области R называется функция y= (x,c), непрерывно дифференциируемая отностительно x и непрерывно относительно c, при условии, что она 1.является решением ДУ при всех значениях c

2.соответствующим выбором значения c функции y= (x,c) дает возможность решить любую задачу Каши в области R.

Частное решение ДУ – это решения, полученные из общего решения при каком-либо конкретном значении произвольной постоянной c. Особое решение – такое решение ДУ, которое во всех своих точках не удовлетворяет свойству единственности.

Замечание: Часто при отыскании общего решения ДУ приходят к уравнению, содержащую произвольную постоянную c и неразрешимому относительно y, т.е. к уравнению , определяющую y, как неявную функцию от x и c. В таких случаях считается, что общее решение ДУ известно, а равенство называется общим интегралом.

3Уравнения с разделяющимися переменными

Уравнение вида называется ДУ с разделяющимися переменными. Пусть f(x) и g(x) непрерывны в промежутке , и при этом . Тогда уравнение такого типа решается следующим образом: . Функции и f(x) непрерывны в соответствующих промежутках, следовательно они имеют первообразные. Интегрируя следующее соотношение получаем:

- общий интеграл ДУ с разделяющимися переменными.

Замечание:

1.К уравнению с разделяющимися переменными относятся уравнения вида:

M(x,y)dx+N(x,y)dy=0: если M(x,y)=m(x)*n(y), N(x,y)=m1(x)*n1(y)

2.Решая уравнения m(x)*n(y)dx+m1(x)*n1(y)dy=0 мы будем решать его на m1(x) и n(y). Однако, если y=y1 есть решение уравнения n(y)=0, то очевидно, что y=y1 – решение данного ДУ. Аналогично, если x=x1 решение уранения m1(x)=0, то x=x1 решение данного ДУ.

Пример: решить ДУ

Решение:

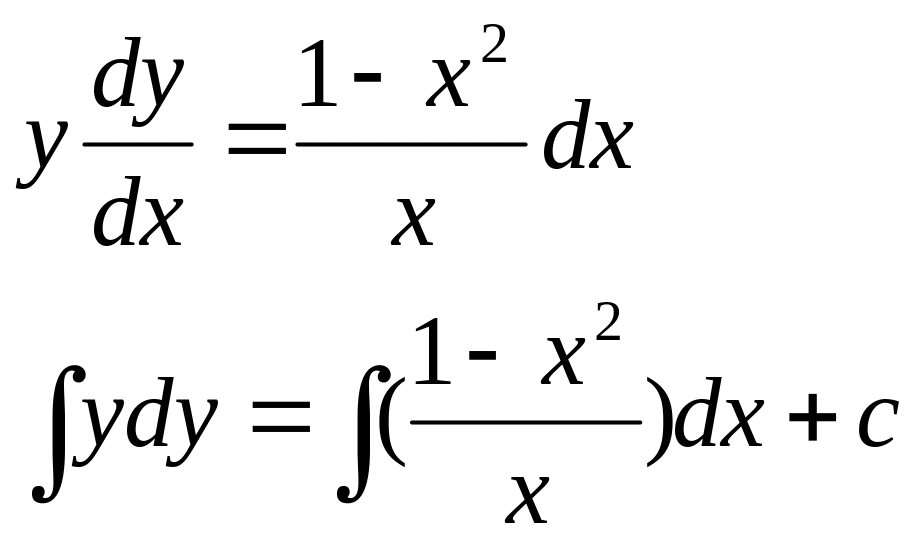
Однородные ДУ 1-ого порядка

Функция f(x,y), определенная на множестве D называется однородной функцией k-ого измерения области D, если для любых значений (x,y) из области D при любых t выполняется равенство:

Пример: f(x,y)=x

дифференциальная функция является однородной функцией 3-его измерения.

Дифференциальное уравнения называется однородным, если f(x,y) – однородная функция 0-ого измерения своих аргументов т.е. f(tx,ty)=f(x,y) (*)

Положим в (*) t=1/x. Тогда получим f(1,y/x)=f(x,y). Функцию, стоящую слева можно рассматривать как функцию 1-ого аргумента y/x. Обозначим эту функцию через . Тогда однородные уравнения можно переписать в виде: . Интегрирование уравнений такого вида с помощью подстановки приводит к уравнению с разделяющимися переменными. В самом деле, пусть u=y/x, тогда y=ux

Тогда y’=u’x+u

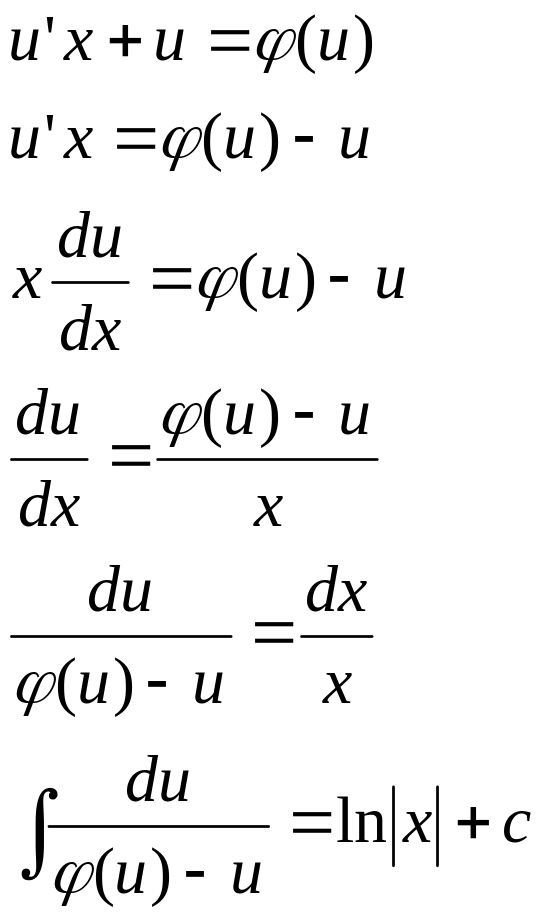
Замечание:

1.Если f(u)-u=0 при некотором значении u=u0, то кроме указанных решений существует также решение ДУ u=u0 или y=u0x или y/x=u0

2.Уравнение вида M(x,y)dx+N(x,y)dy=0 является однородным ДУ 1-ого порядка, если функции M(x,y) и N(x,y) однородные функции одного и того же измерения.

4Линейные ДУ

Уравнение линейное, относительно искомой функции и ее производной называется линейным уравнением 1-ого порядка т.е. уравнением вида:

(1)

Если , то линейное дифференциальное уравнение 1-ого порядка называется однородным, в противном случае уравнение неоднородное. Рассмотрим линейное однородное ДУ 1-ого порядка: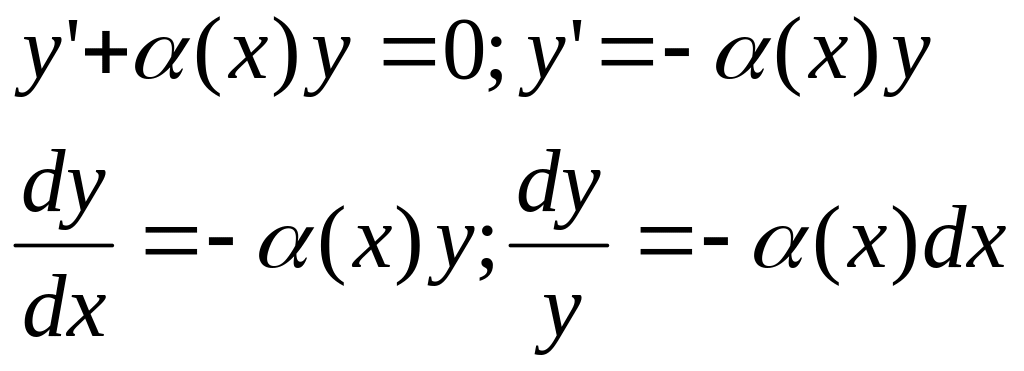

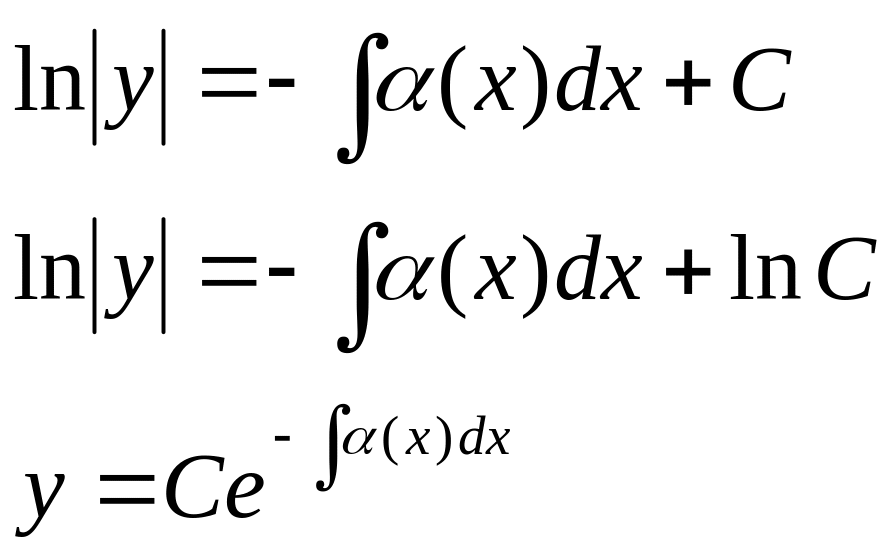
Чтобы найти решение неоднородного уравнения применим метод вариаций произвольной постоянной (метод Лагранжа). Будем искать решение уравнения в виде: (*)

Подставим (*) в уравнение (1):

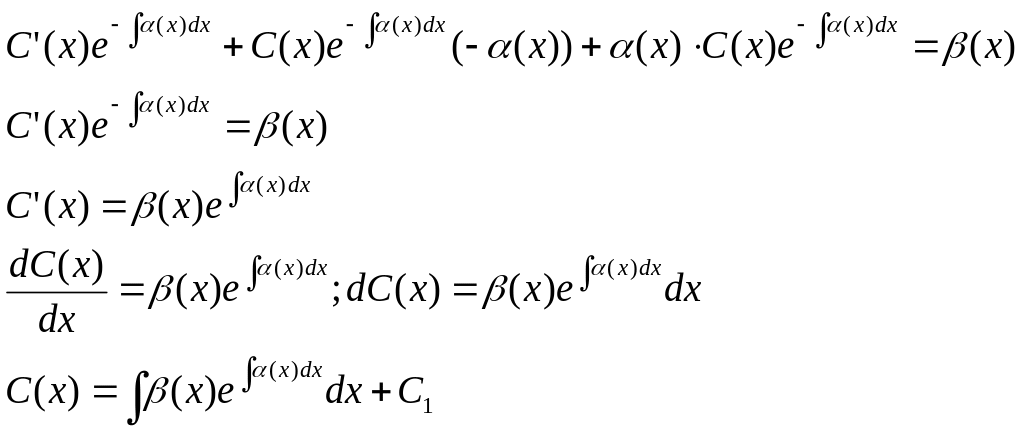
Таким образом, решение линейного неоднородного ДУ 1-ого порядка имеет вид: