Вопрос 14.Формула Грина. Условия независимости криволинейного интеграла 2-го типа от пути интегрирования.

1Формула Грина

Если в функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными 1-ого порядка в области D, то имеет место формула:

- формула Грина, где L - граница области D и интеграл вдоль L ведется в положительном направлении.

2Условия независимости интеграла от линии интегрирования

Для того, чтобы криволинейный интеграл (1)

Не зависел от линии интегрирования необходимо и достатично, чтобы этот интеграл, взятый по замкнутому контуру был равен 0.

Доказательство:

П усть известно, что интеграл (1) не зависит от путей интегрирования. Покажем, что он равен 0 по любому замкнутому контуру

По условию:

Отсюда интеграл по всему замкнутому контуру L:

Обратно. Пусть известно, что интеграл (1) равен 0 по любому замкнутому контуру. Покажем, что он не зависит от линии интегрирования. По условию:

Пусть функции P и Q непрерывны вместе со своими частными производными 1-ого порядка в области D, ограниченной одним замкнутым контуром. Тогда для того, чтобы интеграл (1) не зависел от линии интегрирования необходимо и достаточно, чтобы во всех точках области D соблюдалось равенство:

(2)

Условие (2) равносильно тому, что подынтегральное выражение Pdx+Qdy – полный дифференциал некоторой функции U(x,y) т.е. dU(x,y)=P(x,y)dx+Q(x,y)dy, причем

Но в этом случае вектор есть градиент функции U. Функция U, градиент которой равен вектору называется потенциалом этого вектора. Заметим, что в этом случае:

(3)

Теорему можно сформулировать в следующем виде:

Для того, чтобы интеграл (1) не зависел от линии интегрирования необходимо и достаточно, чтобы его подынтегральное выражение было полным дифференциалом.

Вопрос 15. Алгебраическая форма комплексного числа (определение, операции). Комплексная плоскость. Решение квадратных уравнений во множестве комплексных чисел.

1Определение

Комплексным числом называется выражение вида x+iy, где x,y - действительные числа, i – символ – мнимая еденица, удовлетворяющая соотношению:

(1)

Если y=0, то комплексное число x+i0 считается совпадающим с действительным x.

Если x=0, то комплексное число 0+iy обозначается просо iy – чисто мнимое.

Числа x и y называются соответственно действительной и мнимой частями комплексного числа x+iy и обозначаются символами:

x=Re(x+iy), y=Im(x+iy) (2)

Два комплексных числа z=x+iy, , имеющие одинаковые действительные и противоположные мнимые части называются сопряженными комплексными числами. Будем говорить, что комплексные числа равны

2Операции

1)Сложение

Суммой комплексных чисел называется комплексное число: (3)

Для комплексного числа верны законы сложения (переместительный и сочетательный). Сложение допускает обратную операцию. Для любых комплексных чисел существует комплексное число z, такое что . Это число называется разностью комплексных чисел и и обозначается символом ;

(4)

2)Умножение

Произведением комплексных чисел называется комплексное число (5)

Для комплексных чисел справедливы законы умножения (переместительный, сочетательный, распределительный).

Заметим, что всегда

Умножение так же допускает обратную операцию, если только данный множитель 0

Пусть z 0, тогда существует z, такое что . Для этого согласно формуле (5) надо решить систему уравнений:

, которая всегда при 0 однозначно разрешима.

Это число z называется частным двух чисел и и обозначается . Решая систему, получаем: 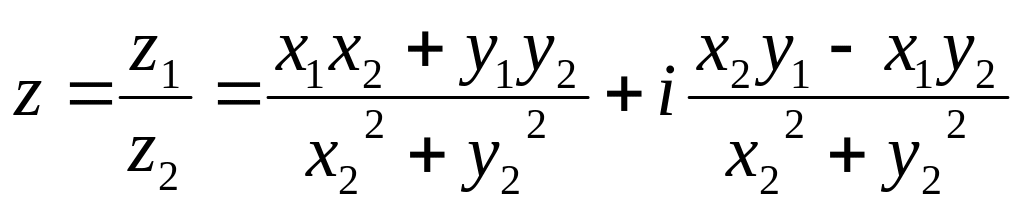(6)

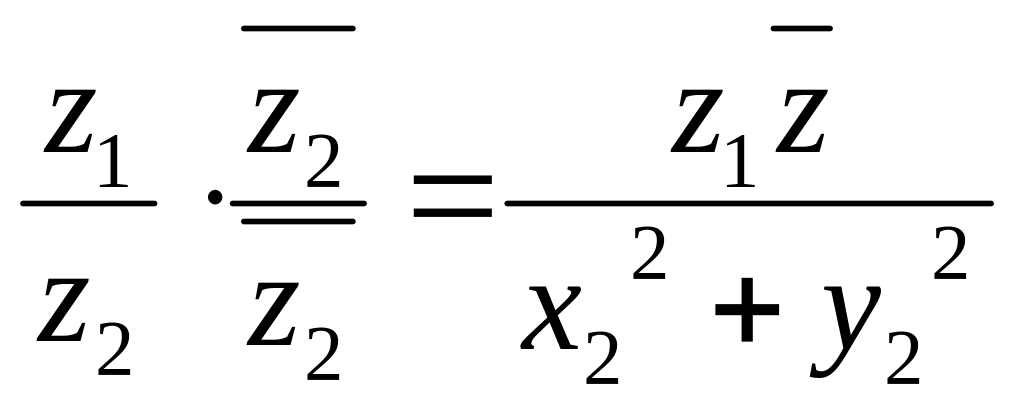
3Комплексная плоскость

Комплексное число x+iy удобно изображать т.(x,y) или соответствующим радиус-вектором на комплексной плоскости. Оси Ox и Oy (в декартовой прямоугольной системе координат) называются соответственно действительной и мнимой осью. Абсцисса и ордината в каждой точке на комплексной плоскости изображаются соответственно. Действительная часть – x и мнимая часть –y комплексного числа z=x+iy. Соответствующие полярные координаты:

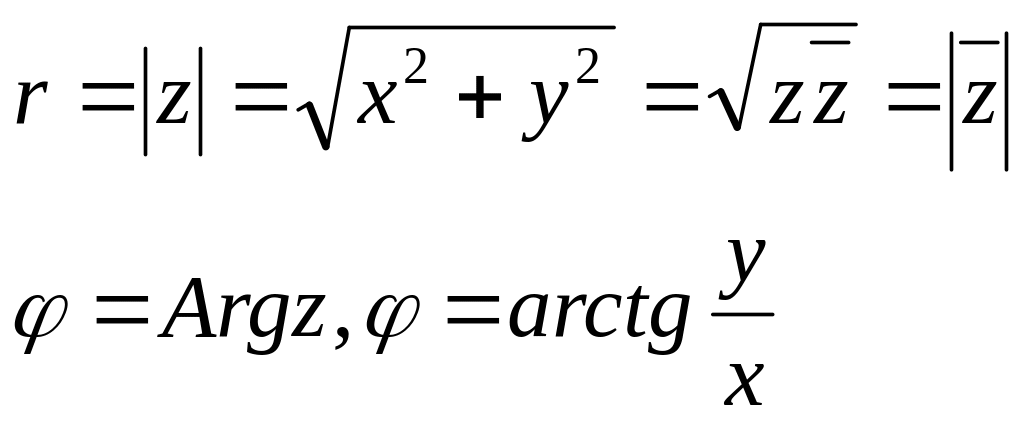
Называются модулем и аргументом комплексного числа z.

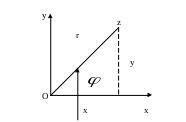
Отметим, что . Отсюда получим тригонометрическую форму комплексного числа: . Выражение x+iy – алгебраическая форма комплексного числа. Аргумент комплексного числа z определяется с точностью до слагаемого 2 , где k – любое целое число. В качестве главного значения Argz (аргумента z) обычно выбирается значение . Главное значение аргумента z обозначается arg z.

4Решение квадратных уравнений в области комплексных чисел: