Вопрос 13. Криволинейный интеграл 2-го типа (по координатам). Свойства и применение. Примеры.

1.Определение:

Пусть точка M движется вдоль некоторой линии L (от точки B к точке C). К точке M приложена сила F(x,y,z)={X(x,y,z) Y(x,y,z) Z(x,y,z)}

Т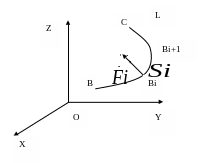 ребуется вычислить работу А силы F при перемещении точки M из положения B в положение C.

Разобьём кривую BC на n произвольных частей точками:

Обозначим через вектор и положим .

Тогда скалярное произведение можно рассмотреть как приближенное выражение работы силы на дуге

Обозначим через приращение координат при переходе от к точке

Тогда ;

Искомая работа: (1)

Если существует предел правой части выражения (1) при , то этот предел выражает работу силы F по кривой L от B до C

(2)

Предел интегральной суммы в правой части (2) называется криволинейным интегралом 2-ого рода от функции X(x,y,z),Y(x,y,z),Z(x,y,z) по кривой L и обозначают:

(3)

2.Свойства криволинейного интеграла.

1)Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак т.к. при этом , а следовательно и его проекции меняют знаки.

2)Если кривая L делится точкой E на 2 дуги L1 и L2 так, что дуга , то

Для обозначения криволинейного интеграла по замкнутому контуру L употребляют символ:

Криволинейный интеграл от векторной функции по замкнутой кривой L называют так же циркуляцией вектора по замкнутому контуру L.

3.Вычисление криволинейного интеграла 2-ого рода

Для того, чтобы вычислить интеграл:

(*)

взятый по линии нужно в подынтегральном выражении заменить x, y, z dx, dy, dz их выражениями через t, dt. Тем самым мы получим обыкновенный интеграл. По интегралу изменения параметра t, соответствующей линии интегрирования:

(*)= ,

Где tB и tC-значения параметра соответственно точек B и C линии L

В случае плоской кривой, уравнение которой задано в виде Y=y(x)

4.Выражение площади области, ограниченной кривой через криволинейный интеграл

Пусть дана правильная область D, ограниченная контуром L. Предположим, что D проектируется на ось X в отрезок [a,b], причем снизу она ограничена кривой L1, уравнение которой , а сверху кривой L2 с уравнением

Тогда площадь области D:

Первый интеграл – криволинейный интеграл по L2 т.к. . Уравнение этой кривой:

Второй интеграл – криволинейный интеграл по L2:

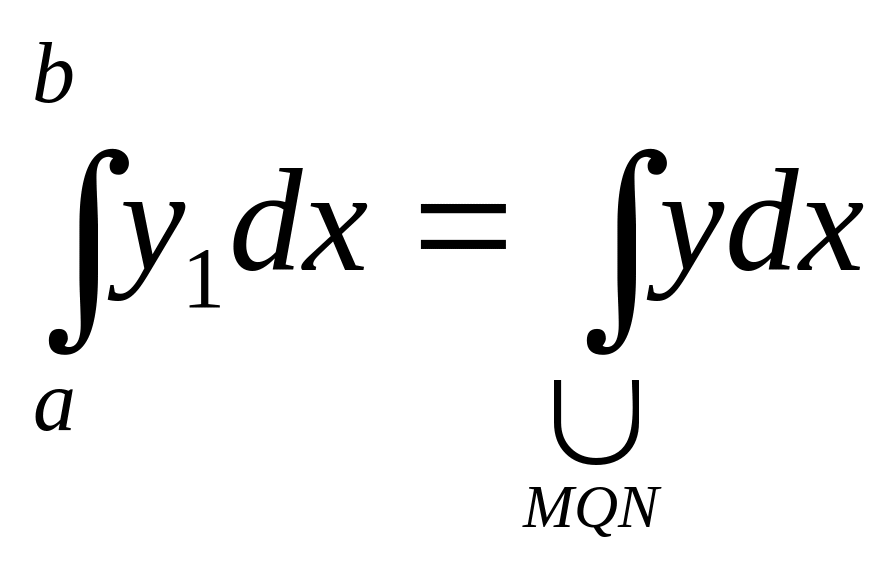
По первому свойству криволинейного интеграла имеем:

При этом кривая L обходится против хода часовой стрелки. Аналогично можно показать, что . Объединяя обе формулы получаем:

4.Нахождение функции по её полному дифференциалу

В случае, если подынтегральное выражение Pdx+Qdy является полным дифференциалом криволинейный интеграл 2-го рода записывается обычно в виде:

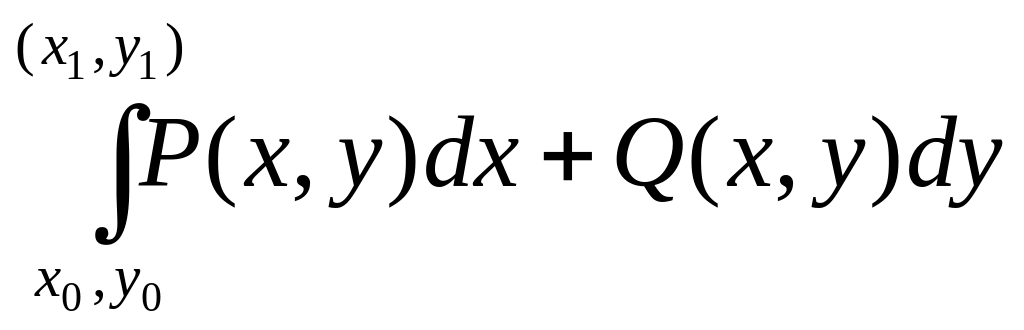(1) , где и - координаты начальной и конечной линии интеграла.

О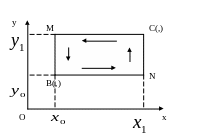 казывается, что целесообразно вычислять интеграл по ломаной BNC, звенья которой параллельны осям координат:

(2)

Аналогичную формулу можно получить и для ломаной BNC. Рассмотрим интеграл с фиксированной начальной точкой и переменной (x,y).

(3)

Величина этого интеграла является функцией координат конечной точки. Будем вычислять интеграл (3) по формуле (2):

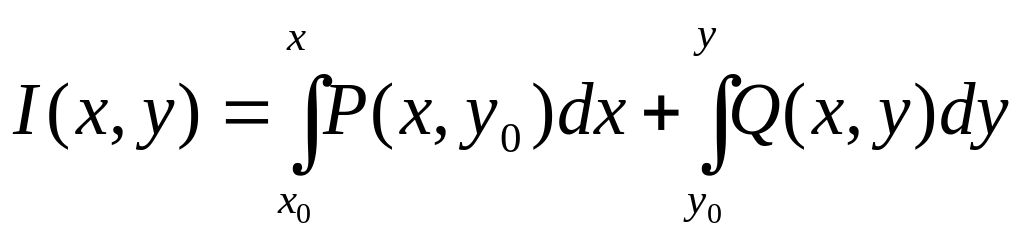
Причём во 2-ом интеграле x считается во время интегрирования постоянным т.к. ,

,то

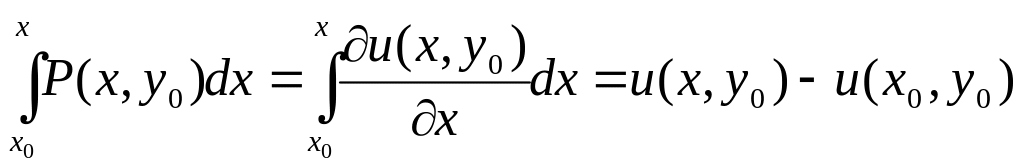
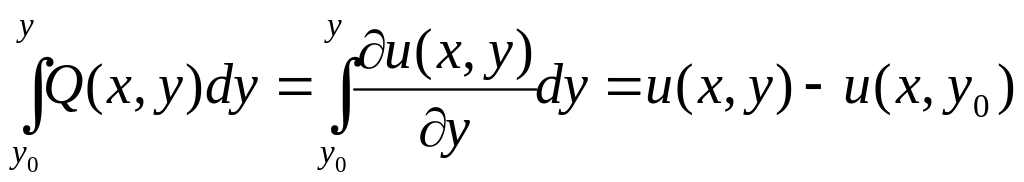
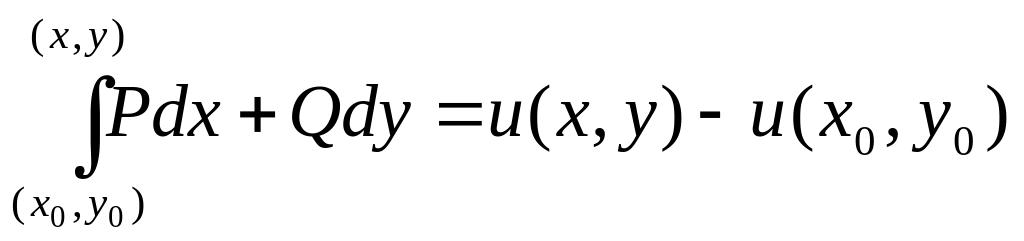(4)

Если назвать функцию U(x,y) назвать первообразной для полного дифференциала Pdx+Qdy, то формула (4) является формулой Ньютона-Лейбница для криволинейных интегралов. Пользуясь полученными результатами иможно указать способ отыскания U(x,y) по её полному дифференциалу:

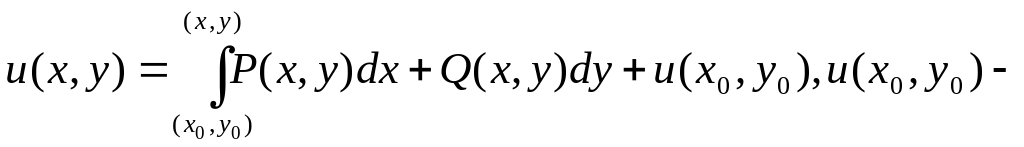произвольная постоянная (5)

Воспользовавшись способами вычисления интеграла (3), рассмотренными выше и заменяя через C получим 2 формулы для вычисления функции u(x,y).

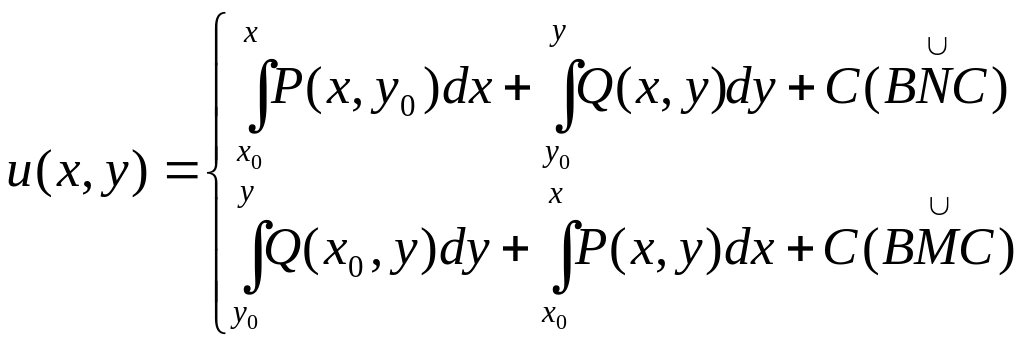(6)

Если в (6) положить C=0, то получим функция U(x,y), обращающуюся в 0 в точке ( ). Начальную точку ( ) следует выбирать так, чтобы подынтегральные функции были, по возможности более простыми.

Найти первообразную функции U(x,y) для полного дифференциала

Решение:

За начальную точку ( ) примем O(0,0).

U(x,y)=