1.3.3. Циклическая структура

Отличительной особенностью этой структуры (рис. 1.3) является наличие в ее составе:

• участка, многократно повторяющегося в процессе вычислений и называемого телом цикла; тело представляет собой типовую линейную или ветвящуюся структуру;

• условия L, предназначенного для своевременного выхода из цикла.

Циклические структуры бывают двух разновидностей: с предусловием, т.е. с проверкой условия выхода из цикла перед выполнением его тела (а) и постусловием, предполагающим проверку указанного условия после выполнения тела цикла (б).

Рис 1.3. Разновидности циклических структур:

а) с предусловием; б) с постусловием

Циклические структуры используются в качестве отдельных элементов в процессе разработки алгоритмов циклических вычислительных процессов (циклов). При этом различают:

1) циклы с заранее известным числом повторений тела или с числом повторений, которое может быть вычислено. Эти циклы называются арифметическими (счетными).

2) циклы с числом повторений, которое заранее неизвестно и подсчитано быть не может - итерационные циклы.

Приступая к организации цикла, необходимо:

• определить, какая переменная будет им управлять или, как говорят, служить его параметром;

• сформулировать закон изменения параметра, т.е. указать, как будет изменяться его величина после каждого повторения тела;

• определить численное значение параметра, при достижении которого необходимо предусмотреть выход из циклической процедуры.

Рассмотрим примеры алгоритмизации циклических вычислительных процессов, упомянутых в п.1.

Пример 1.11

Пусть задана функция y=sin(x2). Необходимо вычислить её значения на отрезке [а,b], если аргумент x меняется на этом отрезке по вполне определённому, заранее заданному, закону. В качестве закона изменения аргумента выберем наиболее простой, но в то же время и чаще всего используемый закон

x_i+1 = x_i + x, i=0,1,2,...,

где x -величина, называемая шагом изменения аргумента. Подставляя в предыдущую формулу значения величины i, получим:

x₁ = x₀ + x; x₂ = x₁ + x; ...,

т.е. каждое следующее значение аргумента x вычисляется путем суммирования его предыдущего значения с шагом x (рис.1.4). Задача, сформулированная таким образом, носит название задачи табулирования функции.

Приступим теперь к разработке алгоритма. В рассматриваемой задаче управляющей переменной (параметром цикла) является аргумент функции, ибо от его текущего значения зависит решение вопроса продолжать ли далее выполнение цикла или закончить вычисления и выйти из него.

Если очередное значение аргумента находится в пределах отрезка [а,b], цикл следует повторить, вычислив при этом соответствующее ему значение функции, в противном случае выйти из цикла.

Поскольку закон изменения параметра сформулирован в постановке задачи, остается определить то значение параметра, при достижении которого циклический процесс следует закончить. Очевидно, что это значение определяется неравенством x_i > b.

Рис. 1.4. Геометрический смысл задачи табулирования функции

Примечание. Если начальным значением аргумента является b и шаг его изменения отрицателен, то условием выхода из цикла будет неравенство x_i < a.

Составим алгоритм нашей задачи, основываясь на следующем:

- начальное значение аргумента вычисляемо функции известно из условия задачи x ₀ = a, следовательно, есть возможность сразу же вычислить соответствующее ему значение функции y ₀.

• очередной шаг - вывод строки таблицы, содержащей значения аргумента и функции;

• далее вычислим очередное значение аргумента, используя при этом закон его изменения на числовой оси x_i+1= x_i+x ;

• полученное значение аргумента x_i сравниваем с его конечным значением b; если оказывается, что x_i > b, то закончим счет задачи, а если нет - перейдем к вычислению очередного значения функции.

Представим алгоритм в виде детализированной и компактной схем.

Детализированная схема алгоритма

К омпактная схема алгоритма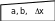

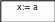
В приведённом алгоритме в линейную структуру вложена циклическая структура с постусловием.

Пример 1.12

Другой подход к решению той же задачи заключается в том, что в качестве параметра цикла используют переменную, называемую счетчиком циклов (в алгоритме, представленном ниже, это переменная j). Начальное значение счетчика принимают равным 1. Этот подход демонстрирует следующий алгоритм.

Схема алгоритма

Перед каждым очередным повторением тела цикла текущее содержимое счетчика автоматически увеличивается на 1 и затем сравнивается с вычисленным заранее конечным значением счетчика. Последнее представляет собой количество повторений тела цикла, которое необходимо выполнить, чтобы решить задачу.

Если текущее значение счетчика цикла не превышает его конечного значения, то выполняется очередное повторение тела цикла, в противном случае операции, составляющие тело цикла, не выполняются, а осуществляется выход из цикла.

Автоматическое выполнение перечисленных операций со счетчиком, включая выход из цикла, предусмотрены символом «подготовка», который располагается всегда в начале циклической части алгоритма.

В предыдущем примере в качестве данных использовались отдельные (их часто называют простыми) переменные.

Однако не для всех задач представление данных в виде простых переменных является рациональным, т.к. на практике часто используют не отдельные величины, а их совокупности.

Поэтому прежде, чем приступить к рассмотрению очередного примера, введем понятие массива (см. также п. 7.4).

Под массивом понимают некоторое множество однородных переменных, каждая из которых имеет свой номер (индекс), который указывает на местоположение данной переменной (элемента) в массиве.

Для того, чтобы отличить один массив от другого, ему присваивается имя.

В зависимости от структуры конкретного массива, т.е. от взаимного расположения его элементов, массивы различают одномерные, двумерные и многомерные.

В этом разделе рассматриваются только одномерные массивы, которые математики называют векторами.

Индекс элемента массива является целочисленной переменной и может принимать положительные, отрицательные или нулевое значения, причем значение индекса каждого следующего элемента массива на единицу больше предыдущего.

Доступ к элементам массива является произвольным. Это означает, что с каждым элементом массива можно производить действия независимо от других элементов. Для этого используют обращение к нужному элементу, которое состоит из имени массива и индекса элемента.

Пример 1.13

Вычислить и записать в массив значения функции y = Ax², при известных значениях x₁, x₂, x₃, x4 и A.

Эта задача отличается от предыдущей тем, что, во-первых, требуемое число повторений цикла известно - их 4; во-вторых, все численные значения аргумента x заданы заранее и их можно представить в виде массива, состоящего из четырех элементов.

В алгоритме параметр цикла i служит одновременно счетчиком выполненных повторений тела цикла и индексом элементов массивов x и y.

Схема алгоритма