- •Центральное и параллельное проецирование
- •Метод двух изображений. Обратимость чертежей
- •Взаимное расположение прямых. Конкурирующие точки.
- •Плоскость. Задание плоскости на чертеже, следы плоскости.
- •Положение плоскости относительно плоскостей проекций.
- •Пересечение плоскостей.
- •Позиционные задачи. Принадлежность точки прямой, точки и прямой плоскости
- •Пересечение прямой и плоскости
- •Проецирование прямого угла.
- •Метрические задачи
- •Классификация метрических задач (определение углов и расстояний)
- •Примеры решения метрических задач
- •Определение длин и углов наклона отрезка прямой к плоскостям проекций.
- •Параллельность и перпендикулярность прямых.
- •Параллельность и перпендикулярность плоскостей
- •Параллельность и перпендикулярность прямой и плоскости.
- •Способы преобразования
- •4.1. Замена плоскостей проекций
- •Метод секущих сфер
- •Метод секущих плоскостей
Пересечение прямой и плоскости
Чтобы построить точку пересечения прямой с плоскостью необходимо:
Заключить прямую во вспомогательную фронтально проецирующую плоскость
Построить линию пересечения плоскостей.
Отметить точку пересечения полученной линией с заданной прямой
Определить видимость прямой относительно плоскости методом конкурирующих точек
Проецирование прямого угла.
Прямой угол проецируеться без искажения если одна его сторона параллельна этой плоскости а другая не перпендикулярна к ней.
Метрические задачи
Классификация метрических задач (определение углов и расстояний)
Решения метрических задач основаны на применении практически всех предыдущих разделов курса начертательной геометрии. Включая прежде всего взаимопринадлежность и пересечение геометрических фигур, параллельность и перпендикулярность и способы преобразования комплексного чертежа.
Поскольку алгоритмы всех разновидностей метрических задач приведены в рабочих тетрадях, то ограничимся их простым перечислением:
Определение расстояний: 1) Между точками. 2) От точки до прямой линии. 3) Между параллельными прямыми. 4) От точки до плоскости. 5) От прямой до плоскости. 6) Между плоскостями. 7) Между скрещивающимися прямыми.
|
Определение углов: 1) Между пересекающимися прямыми. 2) Между скрещивающимися прямыми. 3) Между прямой и плоскостью. 4) Между плоскостями.
|
Примеры решения метрических задач
Простейшие метрические задачи приводились при изучении отдельных предыдущих разделов курса. Теперь рассмотрим несколько относительно сложных задач с применением и почти без применения способов преобразования комплексного чертежа.
Пример1
(Рис.69) Определить расстояние от точки
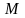 до отрезка
до отрезка
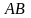 без преобразования чертежа (кроме
заключительной части задачи).
без преобразования чертежа (кроме
заключительной части задачи).
По ходу решения задачи необходимо выполнить три вещи: задать необходимый перпендикуляр, пересечь его с отрезком и определить его натуральную величину этого перпендикуляра.
Задать перпендикуляр – значит найти его точку пересечения с отрезком. С отрезком общего положения. В этом случае перпендикуляр не окажется линией уровня. Поэтому теорема о трех перпендикулярах здесь не поможет. Обратимся к другому пути решения.
Из точки
можно проводить бесконечное множество
прямых, перпендикулярных к отрезку
.
Но только один из них имеет шансы пересечь
отрезок в некоторой точке
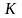 .
Построить точку
можно как результат пересечения отрезка
с плоскостью
.
Построить точку
можно как результат пересечения отрезка
с плоскостью
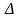 ,
содержащей в себе упомянутые перпендикуляры.
,
содержащей в себе упомянутые перпендикуляры.
Остается
определить длину перпендикуляра
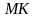 любым способом преобразования чертежа
или способом прямоугольного треугольника
в данной задаче используем способ
вращения вокруг проецирующей прямой.
любым способом преобразования чертежа
или способом прямоугольного треугольника
в данной задаче используем способ
вращения вокруг проецирующей прямой.
|
|
|
1)
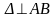 :
:
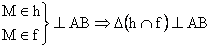
2)
:
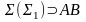 ,
– посредник.
,
– посредник.
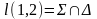
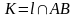
3) – перпендикуляр.
4)
 –
ответ.
–
ответ.
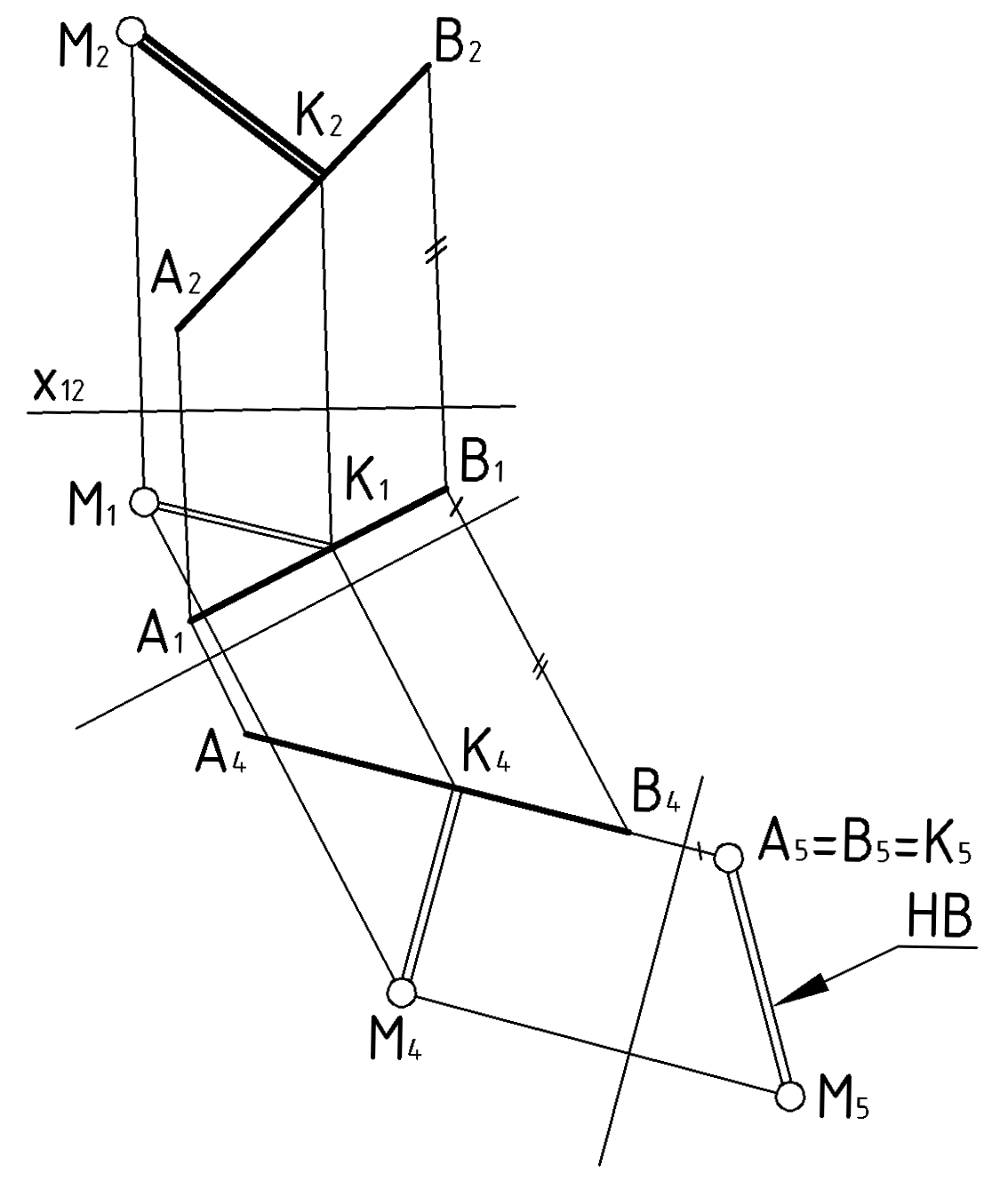
Пример
2 (Рис.70). Решить предыдущую задачу
способом замены плоскостей проекций.
Дополнительно спроецировать перпендикуляр
на
исходные плоскости проекций:
 и
и
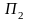 .
.
Чтобы определить длину перпендикуляра , необходимо спроецировать его в натуральную величину. А это станет возможным, если отрезок преобразовать в проецирующую прямую и использовать его вырожденную в точку проекцию. Для решения задачи потребуется две замены плоскостей проекций.
|
|
|
1-я замена:
1.
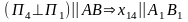
2.
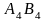 и
,
и
,
AB(A1B1, A4B4) – линия уровня.
2-я замена:
3. (П5
 П4)
AB
П4)
AB
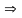 Х45
A4B4,
Х45
A4B4,
4. A5 = B5 и M5,
AB(A4B4, A5=B5) – проецирующая
прямая.
5. |M5, (A5=B5)|=|M,AB| - ответ.
Дополнительно:
при обратном проецировании перпендикуляра
на плоскости
и
учесть,
что в системе плоскость
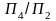 перпендикуляр
– линия уровня.
перпендикуляр
– линия уровня.
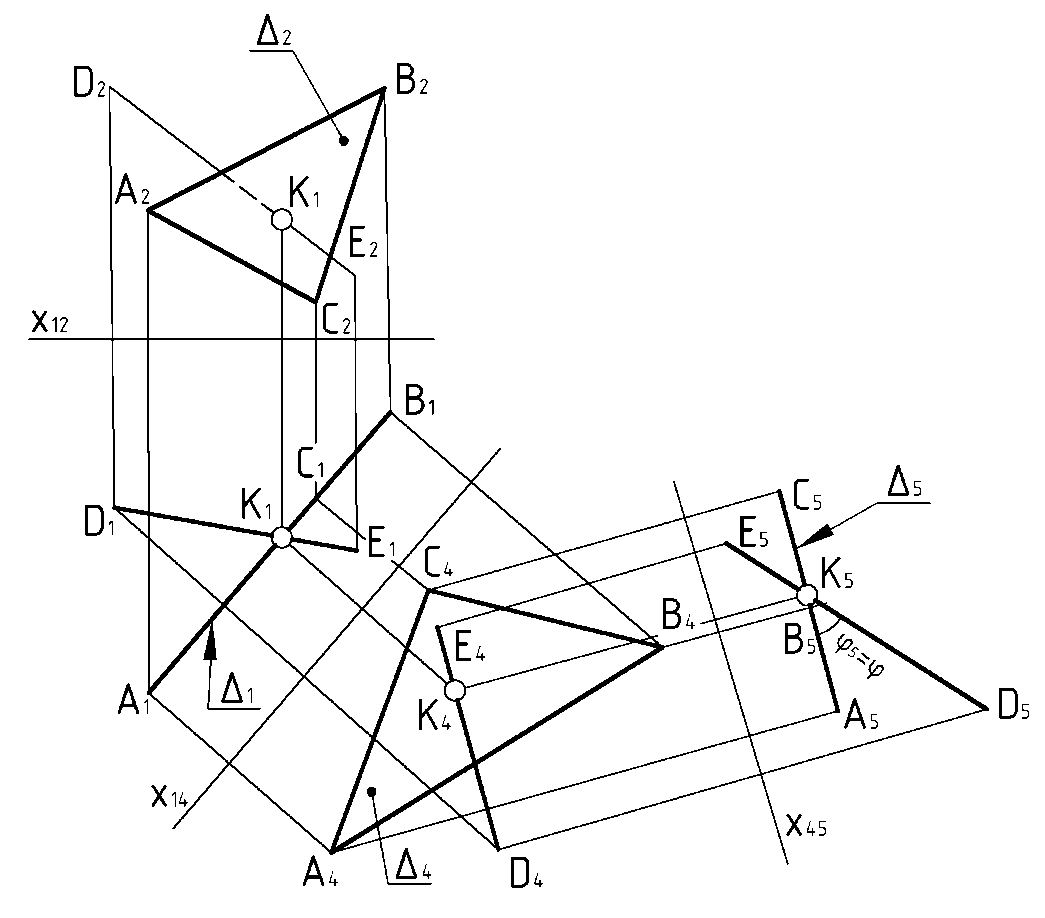
Пример
3 (Рис.71). Определить угол наклона
отрезка
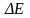 к плоскости
к плоскости
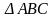 способом замены плоскостей проекций.
способом замены плоскостей проекций.
На чертеже угол между прямой и плоскостью определяется углом между вырожденной проекцией плоскости и натуральной величиной отрезка на прямой. Для получения вырожденной проекции плоскости требуется две замены плоскостей проекций. При второй замене необходимо учитывать, что отрезок в последней системе плоскостей проекций должен оказаться линией уровня.
Решение:
1-я замена:
1.
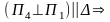
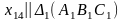
2.
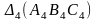 и
и
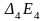 ,
,
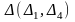 – плоскость уровня.
– плоскость уровня.
|
|
|
3.
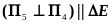
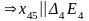 ,
,
4.
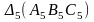 и
и
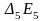 ,
,
 –
проецирующая прямая,
–
проецирующая прямая,
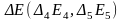 –
прямая уровня.
–
прямая уровня.
5.
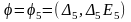 .
.
6. Обводка с учётом видимости.