20. Уравнение моментов.

Момент импульса и момент точки, относительно неподвижного начала О есть векторное произведение

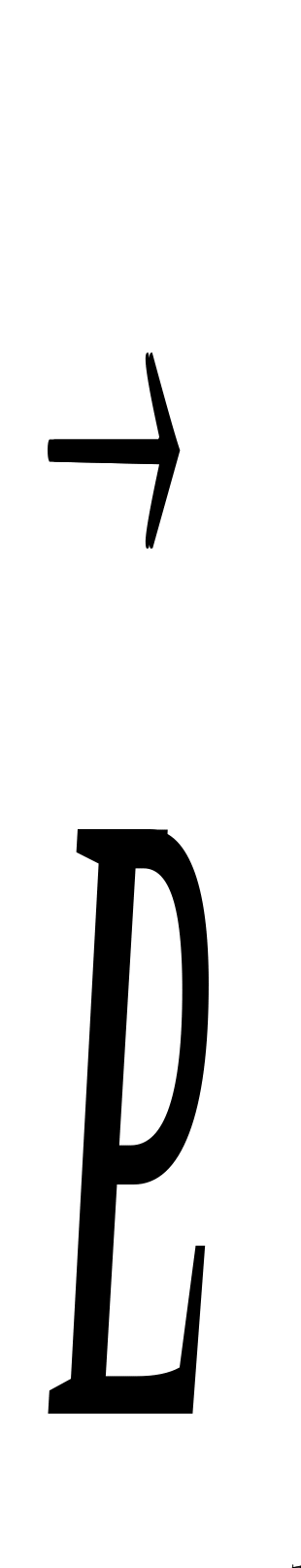
Связь и — ?

— уравнение моментов

Производная по времени момента импульса материальной точки относительно неподвижной точки относительно неподвижного начала равна моменту действующей силы относительно того же начала.

№42. Основное уравнение молекулярно-кинетической теории.

Уравнения состояния идеального газа

И деальный газ удовлетворяет следующим условиям:

1.Объём приходящийся на молекулы

газа, много меньше объёма занятого газа.

2.Радиус взаимодействия двух

молекул значительно меньше

среднего расстояния между ними.

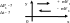(Второй закон Ньютона)

∆P_x=mV_x-(-mV_x)=2mV_x

— средняя сила, первой молекулы

д ля N — молекул, — средняя

— средняя скорость

называется средней квадратичной скоростью в направлении оси ОХ.

нет выделенных направлений в пространстве.

— основное уравнение молекулярно кинетическая теория

№41. Диспергирующая среда. Нормальная и аномальная дисперсия.

Груповая скорость. Волновой поток.

Опр: Суперпозиция (наложение) волн мало отличающихся друг от друга по частоте называется волновым пакетом или групповой олн.

— волновой пакет

С корость максимума амплитуды волнового пакета, называется групповой скоростью.

Ф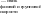 ронтальная скорость:

Групповая скорость:

Среда для которой положительная (>0) для нее

U < V — этот случай называется случай нормальной дисперсии,

U > V — аномальной дисперсии.

Для вакуума скорость U и скорость V они одинаковы (U=V).

№28. Малые колебания. Дифференциальные уравнения для свободных колебаний (без затухания, с затуханием) и вынужденных колебаний.

Колебательное движение

Колебаниями называются процессы отличающиеся той или иной степенью повторяемости.

В зависимости от физической природы повторяющегося процесса различают колебания механические, электромагнитные, электромеханические и др. В зависимости от характера воздействия на колеблющуюся систему различают свободные или собственные колебания, вынужденные, автоколебания, параметрические колебания.

Свободы или собственными называются такие колебания которые происходят в системе предоставленные самой себе, после того как ей был совершён толчке, либо она была выведена из положения равновесия.

Вынужденными называются такие колебании в процессе которых колеблются система подвергается воздействию внешней периодичности изменяющейся силе.

Гармонические колебания — это такие колебания, при которых колеблющаяся система и величина которая её характеризует изменяется со временем по закону синуса или косинуса.

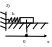Второй закон Ньютона:

ma=F_упр

F_упр= -kx

m = -kx

• Дифференциальное уравнение свободных не затухающих колебаний

k – коэффициент упругости, m – масса

x = a cos(ω₀t + α)

(ω₀t + α) — фаза колебаний

ω₀ — частота собственных колебаний

Т — период колебаний

а — амплитуда колебаний

В еличина наибольшего отклонения системы от положения равновесия называется амплитудой колебания.

циклическая

ω = 2π

— круг

а — константа

α — начальные условия

И мак смещение х изменяется со временем по закону косинуса (или синуса), следовательно движением системы находящейся под действием упругой силы приставляет собой гармоническое колебание.

№34. Полная энергия колеблющейся системы.

. — постоянная угловая скорость

Потенциальная и кинетическая энергии тела даются выражениями

Каждая из них меняется во времени. Однако их сумма E во времени должна оставаться постоянной:

.

Если воспользоваться выражением (6.1), то из формул (6.11) найдем

,

или в силу соотношения (6.9)

.

Эти формулы можно также записать в виде

.

Они показывают, что кинетическая и потенциальная энергии в отдельности не остаются постоянными, а совершают гармонические колебания вокруг общего среднего значения с удвоенной круговой частотой . Когда кинетическая энергия проходит через максимум, потенциальная обращается в нуль и обратно. Однако полная энергия остается постоянной и связана с амплитудой a соотношением

Все изложенное здесь применимо к гармоническим колебаниям любых механических систем с одной степенью свободы. Мгновенное положение механической системы с одной степенью свободы может быть определено с помощью какой-либо одной величины q, называемой обобщенной координатой, например, угла поворота, смещения вдоль некоторой линии и пр. Производная обобщенной координаты по времени называется обобщенной скоростью. При рассмотрении колебаний механических систем с одной степенью свободы за исходное удобнее брать не уравнение движения Ньютона, а уравнение энергии. Допустим, что механическая система такова, что ее потенциальная и кинетическая энергии выражаются формулами вида

где  и  – положительные постоянные (параметры системы). Тогда закон сохранения энергии приводит к уравнению

Оно отличается от уравнения (6.12) только обозначениями, что при математическом рассмотрении не имеет значения. Из математической тождественности уравнений (6.12) и (6.15) следует, что и общие решения их одинаковы. Поэтому, если уравнение энергии приводится к виду (6.15), то

т.е. обобщенная координата q совершает гармоническое колебание с круговой частотой