3. Динамика вращательного движения. Момент инерции. Момент импульса. Закон сохранения импульса.

Момент инерции материальной точки относительно некоторой оси равен произведению ее массы на квадрат расстояния от точки до этой оси I=m*R². момент инерции тела есть сумма моментов инерции материальных точек, составляющих тело. Он может быть выражен через массу тела и его размеры. Теорема Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния между осями.

При равномерном вращательном движении сумма моментов действующих на тело сил равна нулю.

Согласно второму закону Ньютона, сила действующая на тело м

F

Для вращательного движения можно записать что

Момент инерции тела числен­но равен сумме произведений масс всех его точек на квадраты их рас­стояний до оси вращения. Величина момента инерции зависит не только от массы всего тела и ее распределения в теле, но также от его ориентации относительно оси вращения.

-общий вид

Если сопоставить это уравнение с известной формулой закона Ньютона, то мы увидим что для вращательного движения вместо силы имеет место момент силы, вместо массы –момент инерции, вместо ускорения – угловое ускорение.

Моменты инерции тел разной формы.

Шар:

Диск:

Обод: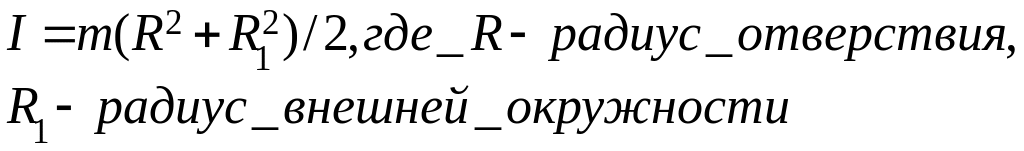

Стержень: -для случая, когда ось вращения проходит через половину длины стержня момент инерции стержня равен. Здесь l- длина стержня

Формула Штейнера

Если известен момент инерции тела относительно оси проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется формулой Штейнера.

Формула Штейнера гласит: момент инерции тела относительно произвольной оси равен моменту инерции относительно параллельной оси проходящей через центр масс плюс произведения массы тела на квадрат расстояния между осями т.е.

2 закон Ньютона для вращательного движения можно выразить через импульс тела.

Произведение массы тела на его спорость называют импульсом {или количеством движения) тела. Импульс тела — векторная величина, так как скорость — вектор.

Момент импульса – векторная величина, численно равная произведению импульса тела на плечо r: I=m*v*r=p*r. Векторная сумма моментов импульсов тел, входящих в замкнутую систему, есть величина постоянная – закон сохранения момента импульса. Для системы, состоящей из любого числа тел, суммарный импульс системы остается постоянным, если только внешние силы отсутствуют.

4. Молекулярная физика. Статистический подход в молекулярной физике. Термодинамика. Термодинамические параметры.

Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя из так называемых молекулярно-кинетических представлений. Согласно этим представлениям, любое тело — твердое, жидкое или газообразное, состоит из большого количества весьма малых обособленных частиц — молекул. Молекулы всякого вещества находятся в беспорядочном, хаотическом, не имеющем какого-либо преимущественного направления движении. Его интенсивность зависит от температуры вещества.

Молекулярно-кинетическая теория ставит себе целью истолковать те свойства тел, которые непосредственно наблюдаются опыте (давление, температуру и т. п.), как суммарный результат действия молекул. При этом она пользуется статистическим методом интересуясь не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое ее название — статистическая физика.

Изучением различных свойств тел и изменений состояния вещества занимается также термодинамика. Однако в отличие молекулярно-кинетической теории термодинамики изучает микроскопические свойства тел и явлений природы, не интересуясь микроскопической картиной. Не вводя в рассмотрение молекулы и атомы, не входя в микроскопическое рассмотрение процессов, тер­модинамика позволяет делать целый ряд выводов относительно их протекания.

В основе термодинамики лежит несколько фундаментальных законов (называемых началами термодинамики), установленных на основании обобщения большой совокупности опытных фактов. В силу этого выводы термодинамики имеют весьма общий характер.

Подходя к рассмотрению изменений состояния вещества с различных точек зрения, термодинамика и молекулярно-кинетическая теория взаимно дополняют друг друга, образуя по существу одно целое.

Обращаясь к истории развития молекулярно-кинетических представлений, следует прежде всего отметить, что представления об атомистическом строении вещества были высказаны еще древними греками. Однако у древних греков эти идеи были не более чем ге­ниальной догадкой. В XVII в. атомистика возрождается вновь, но уже не как догадка, а как научная гипотеза. Особенное развитие эта гипотеза получила в трудах гениального русского ученого и мыслителя М. В. Ломоносова (1711 — 1765), который предпринял попытку дать единую картину всех известных в его время физических и химических явлений. При этом он исходил из корпускулярного (по современной терминологии — молекулярного) представления о строении материи. Восставая против господствовавшей в его время теории теплорода (гипотетической тепловой жидкости, содержание которой в теле определяет степень его нагретости), Ломо­носов «причину тепла» видит во вращательном движении частиц тела. Таким образом, Ломоносовым были по существу сформули­рованы молекулярно-кинетические представления.

Во второй половине XIX в. и в начале XX в. благодаря трудам ряда ученых атомистика превратилась в научную теорию.

Статистика изучает количественные характеристики массовых явлений. В одном сантиметре кубическом в газовом состояние при нормальных условиях содержится 2.7*10 молекул, а в конденсированном состояние порядка 10 частиц. Следовательно мы имеем дело с макроскопическими системами Макроскопические св-ва систем состоящих из очень большого числа частиц изучаются статистическими методами основанные на теории вероятности и на определённых моделях строения изучаемых систем. В совокупном поведении большого числа частиц проявляются особые закономерности, которые называются статистическими закономерностями несмотря на то, что каждая отдельная частица подчиняется законам механики, но оно подчиняется законам статистической физики и термодинамики.

Термодинамика – не учитывает строение вещества или системы а также характер движения отдельной частицы, но рассматривает различные превращения энергии системы в целом изучает физические свойства системы. Термодинамические параметры. Для описания состояния термодинамической системы введены термины параметры, параметры состояния системы. Термин параметры давление, удельный объём и температура