2.4 Поверочный тепловой расчет

На практике часто возникает необходимость для стандартного или вновь разработанного теплообменника при известных расходах G1, G2, начальных температурах t1´и t2´ , площади поверхности аппарата F определить конечные значения температур теплоносителей t1´´и t2´´ или, что то же самое, тепловую мощность аппарата. Из курса тепломассообмена [34, 35] известно, что t1´´и t2´´ можно рассчитать по формулам

где ε – эффективность теплообенника, определяемая долей его действительной тепловой мощности от максимально возможной; (Gс)мин – наименьшее из G1с1 и G2с2.

Из курса тепломассообмена и теории теплообменных аппаратов известно также, что в случае прямотока совместное решение уравнений теплопередачи и теплового баланса с учетом уравнения (2.25) дает следующее выражение для эффективности:

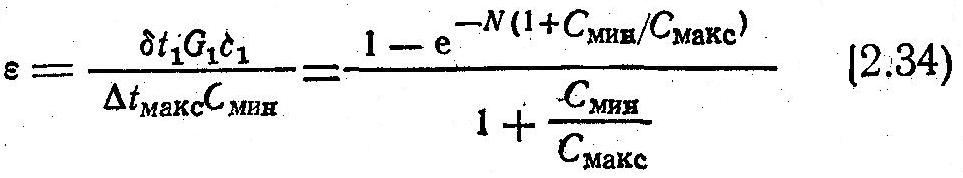
где δ t1= t1´- t1´´; ∆ tмакс= t1´- t2´; N=F/Cмин – число единиц переноса; Смин, Смакс – наименьшая и наибольшая полные теплоёмкости теплоносителей, равные соответственно наименьшему и наибольшему произведениям расходов теплоносителей на их удельные теплоёмкости.

В случае противотока

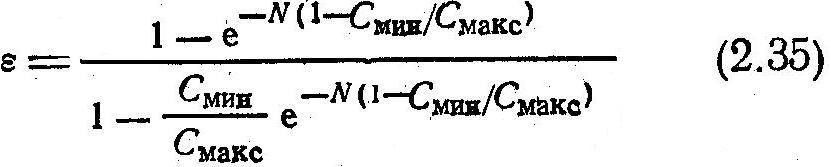
Для перекрестной и более сложных схем движения теплоносителей зависимости

ε (N, Смин/Смакс) приведены в [50,58].

Если коэффициент теплопередачи заранее неизвестен, его вычисляют так же, как при проведении теплового конструктивного расчета.

При Смакс>>Смин (например, в случае конденсации пара, охлаждаемого водой)

Этим, в частности, можно подтвердить отсутствие влияния на ∆ t схемы движения теплоносителей при Смакс/Смин-->к бесконечности.

Из уравнений теплопередачи и теплового баланса следует также, что

N1=F/C1= δ t1/∆ t и N2=F/C2= δ t2/∆ t; ε1= δ t1/∆ tмакс и ε2= δ t2/∆ tмакс, а ε1=ε2С2\С1. Поэтому по аналогии с формулами (2.34) и (2.35) могут быть получены зависимости вида ε1(N1, С1,С2) и ε2(N2, С1,С2).

Необходимость использовать для каждой конкретной схемы дви­жения теплоносителей свою, отличную от других формулу эффектив­ности затрудняет проведение расчетов. Для устранения отмеченного недостатка можно воспользоваться методом ф-тока. В соответствии с этим методом зависимость эффективности ε2 от числа единиц переноса N ₂ и относительной полной тепло­емкости ω=С₂/С1 для всех без исключения схем движения теплоноси­телем описывается единой формулой

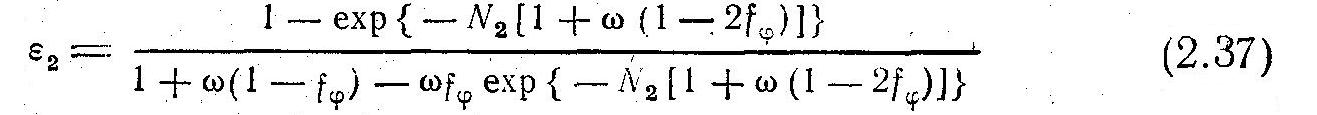
где f_ф— характеристика схемы тока. Легко видеть, что при f_ф=0 фор­мула (2.37) переходит в формулу (2.34) для прямотока, при f_ф =1 — в формулу (2.35) для противотока.

Идея метода ф-тока основана на том, что значения эффективности для подавляющего большинства сложных схем лежат между значения­ми эффективности для прямотока и противотока. Тогда, вводя функ­цию f_ф = 0,5(1—cosф), при ф=0 получаем f_ф =0, т. е. минимальное значение характеристики схемы тока, которое соответствует прямотоку. При f_ф =π имеем максимальное значение характеристики f_ф =1, кото­рое отвечает наиболее эффективной противоточной схеме.

Для любой схемы, кроме прямоточной и противоточной, для кото­рой f_ф — величины постоянные, f_ф есть, как правило, некоторая функ­ция от N2=F/C2. Однако расчеты показали, что при N2≤1,5 и даже при N2≤2 f_ф можно принимать постоянными. Значения этих постоян­ных приведены в табл. 2.3. Там же даны предельные значения харак­теристик схемы тока f_ф *, которые получаются, если в формуле (2.37) осуществить предельный переход при N2—>°° и ω—>1:

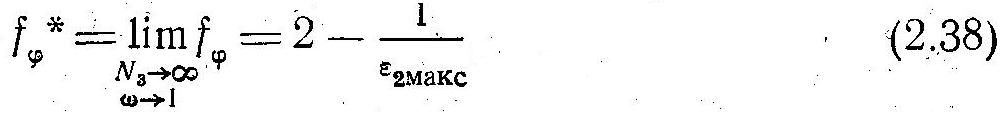
При использовании уравнения (2.37) появляется возможность про­водить на ЭВМ расчеты теплообменников с различными схемами движения теплоносителей по единообразной методике. При этом любой из теплообменных аппаратов можно представить в виде схемы, содержа­ щей параллельно и последовательно включенные элементарные теплообменники, в каждом из которых движение теплоносителей носит только либо прямоточный, либо противоточный, либо поперечно-точ­ный, либо перекрестно-точный характер, т. е является простым. Раз­ меры элементарных теплообменников всегда выбирают достаточно малыми, чтобы можно было пренебречь нелинейным характером изме­нения температуры теплоносителей и рассчитывать средний температурный напер на каждом из элементарных участков поверхности как среднеарифметический.

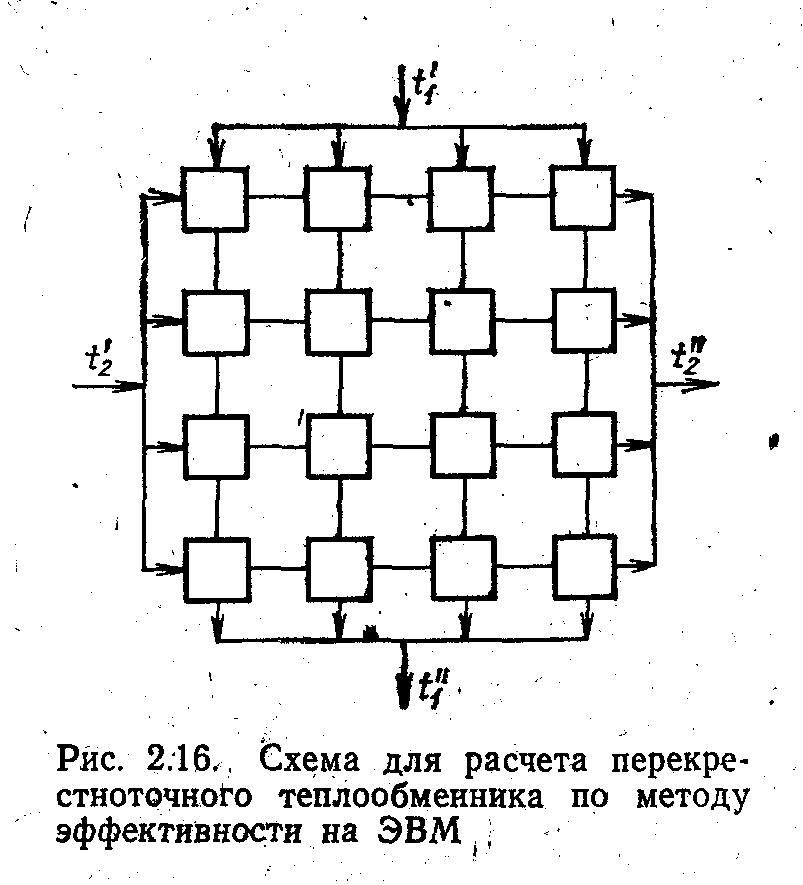
Пользуясь методом эффективности, удобно проводить не только по­верочные, но и тепловые конструктивные расчеты теплообменников с самыми различными схемами движения теплоносителей. Для примера рассмотрим последовательность расчета перекрестноточного теплообменного аппарата.

Разобьем поверхность теплообменника на i элементарных участков, как показано на рисунке 2.16. Участки выберем достаточно малыми, чтобы в пределах каждого из них выполнялись условия N2=δ t2/∆ t<2 и ∆ t=0.5(∆ tб+∆ tм).При этом f_ф =постоянная величина. Кроме того, считая коэффициент теплопередачи неизменным вдоль всей поверхности, при С2=const имеем F/Cмин= const, если одинаковы площади поверхностей всех элементарных участков Fi. Тогда последовательность расчета теплообменника выглядит следующим образом.

1. Вычисляют эффективность всего теплообменника по заданным начальным и конечным температурам теплоносителей.

2. Выбирают некоторое значение для ступеней, причем, где (N2i)1=N2, N2 - число едениц переноса всей системы.

3. По уравнению (2.37) вычисляют эффективность каждой ступени.

4. По рассчитывают конечные значения (t1´´)1 и (t2´´)1 Если они не совпадают с заданными t1´´ и t2´´ , изменяют принятое значение .

5. В случае их совпадения находят полную площадь поверхности теплообмена

F= N2*C2/.

Используя изложенный метод, можно вычислить значения характеристик f_ф для всех приведенных в таблице 2.3 и не вошедших в нее схем течения для любых значений N2 во всём диапазоне их изменения.