
- •Отношения между множествами
- •Основные операции над множествами
- •Билет 2 Счётные множества
- •Счетность множества рациональных чисел.
- •Билет 3
- •Билет 4 Определение иррационального числа
- •Множество действительных чисел
- •Расширенная числовая прямая
- •Билет 5 Ограниченные и неограниченные множества
- •Верхняя и нижняя грань множества
- •Билет 6 Числовая последовательность
- •Ограниченные и неограниченные последовательности
- •Билет 7 Бесконечно большие и бесконечно малые последовательности
- •Билет 8 Сходящиеся последовательность
- •Билет 9
- •Билет 10
- •Билет 11
Расширенная числовая прямая
Расширенная
числовая прямая ![]() (читается «эр с чертой») — множество
вещественных чисел
(читается «эр с чертой») — множество
вещественных чисел
![]() , дополненное двумя элементами:
, дополненное двумя элементами:
![]() (положительная бесконечность) и
(положительная бесконечность) и
![]() (отрицательная бесконечность), то есть
(отрицательная бесконечность), то есть
![]()
Бесконечности
и
, которые не являются числами в обычном
понимании этого слова, также называют
бесконечными числами, в отличие от
вещественных чисел
![]() , называемых конечными числами. При этом
для любого вещественного числа
, называемых конечными числами. При этом
для любого вещественного числа
![]() по определению полагают выполненными
неравенства
по определению полагают выполненными
неравенства
![]()
Cледует
отличать расширенную числовую прямую
от множества вещественных чисел,
дополненного одной бесконечностью
![]() . Такая система называется проективной
прямой, и обозначается
. Такая система называется проективной
прямой, и обозначается
![]()
Билет 5 Ограниченные и неограниченные множества
Множество Е
точек на прямой может либо состоять из
точек, расстояния которых от начала
координат не превосходят некоторого
положительного числа, либо иметь точки,
сколь угодно далекие от начала координат.
В первом случае множество Е называется
ограниченным, а во втором — неограниченным.
Примером ограниченного множества может
служить множество всех точек отрезка
![]() ,
а примером неограниченного
множества—множество всех точек с целыми
координатами.
,
а примером неограниченного
множества—множество всех точек с целыми
координатами.
Нетрудно
видеть, что если а — фиксированная точка
на прямой, то множество Е будет ограничено
в том и только в том случае., если
расстояния от точки а до любой точки
![]() не превосходят некоторого положительного
числа.
не превосходят некоторого положительного
числа.
Верхняя и нижняя грань множества
Наименьшее среди всех чисел, ограничивающих сверху числовое множество Е R, называется его верхней гранью и обозначается β = sup E, то есть
1:
![]() x E: x ≤ β,
x E: x ≤ β,
2:
ε > 0![]() x
x
![]() E: x > β - ε.
E: x > β - ε.
Наибольшее
среди всех чисел, ограничивающих числовое
множество Е![]() R, называется его нижней гранью и
обозначается α = inf E, то есть
R, называется его нижней гранью и
обозначается α = inf E, то есть
1: x E: x ≥ α,
2: ε > 0 x E: x < α + ε.
Билет 6 Числовая последовательность
Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Определение
Пусть множество
X — это либо множество вещественных
чисел R , либо множество
комплексных чисел C . Тогда
последовательность
![]() элементов множества X называется
числовой последовательностью.
элементов множества X называется
числовой последовательностью.
Примеры
Функция
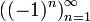 является бесконечной последовательностью
целых чисел. Начальные отрезки этой
последовательности имеют вид
является бесконечной последовательностью
целых чисел. Начальные отрезки этой
последовательности имеют вид
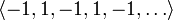 .
.Функция
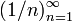 является бесконечной последовательностью
рациональных чисел. Начальные отрезки
этой последовательности имеют вид
является бесконечной последовательностью
рациональных чисел. Начальные отрезки
этой последовательности имеют вид
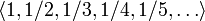 .
.Функция, сопоставляющая каждому натуральному числу
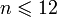 одно из слов «январь», «февраль»,
«март», «апрель», «май», «июнь», «июль»,
«август», «сентябрь», «октябрь»,
«ноябрь», «декабрь» (в порядке их
следования здесь) представляет собой
последовательность вида
одно из слов «январь», «февраль»,
«март», «апрель», «май», «июнь», «июль»,
«август», «сентябрь», «октябрь»,
«ноябрь», «декабрь» (в порядке их
следования здесь) представляет собой
последовательность вида
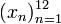 . В частности, пятым членом x5
этой последовательности является слово
«май».
. В частности, пятым членом x5
этой последовательности является слово
«май».
Операции над последовательностями
На множестве всех последовательностей элементов множества X можно определить арифметические и другие операции, если таковые определены на множестве X. Такие операции обычно определяют естественным образом, т. е. поэлементно.
Пусть
на множестве X определена N-арная операция
f:
![]()
Тогда
для элементов
![]() ,
,
![]() , …,
, …,
![]() множества всех последовательностей
элементов множества Xоперация f будет
определяться следующим образом:
множества всех последовательностей
элементов множества Xоперация f будет
определяться следующим образом:
![]()
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых последовательностей (xn) и (yn) называется числовая последовательность (zn) такая, что zn = xn + yn.
Разностью числовых последовательностей (xn) и (yn) называется числовая последовательность (zn) такая, что zn = xn − yn.
Произведением
числовых последовательностей xn и yn
называется числовая последовательность
(zn) такая, что
![]() .
.
Частным
числовой последовательности xn и
числовой последовательности yn, все
элементы которой отличны от нуля,
называется числовая последовательность
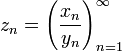 . Если в последовательности yn на позиции
. Если в последовательности yn на позиции
![]() всё же имеется нулевой элемент, то
результат деления на такую последовательность
всё равно может быть определён, как
последовательность
всё же имеется нулевой элемент, то
результат деления на такую последовательность
всё равно может быть определён, как
последовательность
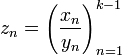 .
.
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.
