29. Ламинарное течение жидкости.

Ламина́рное тече́ние (лат. lamina — пластинка, полоска) — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе  .

В некоторых случаях для получения порогового числа Рейнольдса достаточно провести линейный анализ устойчивости — теоретический анализ устойчивости под воздействием бесконечно малых возмущений. Так, например, получены пороги для течения между параллельными плоскостями и течения Тейлора между вращающимися цилиндрами. Однако в некоторых случаях линейного анализа недостаточно: для течения в круглой трубе он приводит к абсолютной устойчивости, что опровергается экспериментами.

В гидравлике, если труба некруглого сечения, то Re_кр рассчитывается по гидравлическому диаметру dг=4F/χ, где F — площадь поперечного сечения трубы, χ — полный смоченный периметр.

30. Вязкое трение при турбулентном движении жидкости.

нет ответа

31. Турбулентное течение в шероховатых трубах.

Исследование течения жидкости в шероховатых трубах практически полностью основываются на экспериментальных исследованиях. На их результатах основаны зависимости и расчётные формулы, применяющиеся для определения потерь энергии в подобных условиях. Основная формула для определения потерь напора – формула Дарси. Отличие заключается только в коэффициенте потерь на трение. В отличие от турбулентных потоков в гладких трубах, где коэффициент на трение   полностью определяется числом Рейнольдса Re, для потоков в трубах имеющих шероховатые внутренние поверхности   зависит ещё и от размеров этой шероховатости. Установлено, что решающее значение имеет не абсолютная высота неровностей (абсолютная шероховатость) k, а отношение высоты этих неровностей к радиусу трубы r0. Эта величина обозначается    и называется относительной шероховатостью. Одна и та же абсолютная шероховатость может практически не влиять на коэффициент трения в трубах большого диаметра, и существенно увеличивать сопротивление в трубах малого диаметра. Кроме того, н а сопротивление потоку жидкости влияет характер шероховатости. По характеру шероховатость разделяют на естественную, при которой величина неровностей k по длине трубы различна, и регулярную, при которой размеры неровностей по всей трубе одинаковы. Регулярная шероховатость создаётся и скусственно и характеризуется тем, что имеет одинаковую высоту и форму неровностей по всей длине трубы. Шероховатость такого вида называют равномерно распределённой зернистой шероховатостью. Коэффициент потерь на трение в этом случае описывается функцией

.

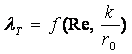На практике для определения потерь напора в реальных шероховатых трубах чаще всего используют формулу Альдшуля

.

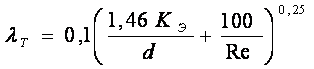Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения. В этих местах интенсивно теряется напор. Примерами местных сопротивлений могут быть искривления оси трубопровода, изменения проходных сечений любых гидравлических аппаратов, стыки трубопроводов и т.п. Потери напора на местных сопротивлениях  определяются по формуле Вейсбаха:

;

где    - коэффициент местного сопротивления.