5.2. Схемы на оу

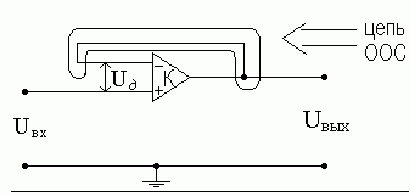
1. Повторитель напряжения.

, т.к. (см. примечание ниже). По 2-ому закону Кирхгофа: т.к. , то .

ООС, последовательная по входу, сто процентная по напряжению. Сигнал подключается к неинвертирующему входу ОУ.

Примечание: при анализе всех схем на ОУ будем считать ОУ идеальным.

Такая схема на ОУ является повторителем напряжения, т.к. , и повторяет входное напряжение по фазе и по величине. Таким образом «К» схемы равен единице.

2. Неинвертирующий усилитель.

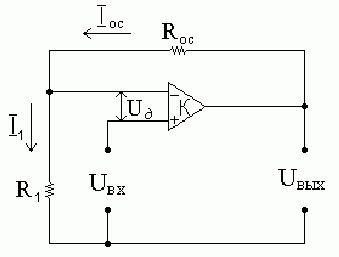
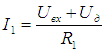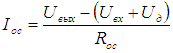Сигнал подаётся на неинвертирующий вход, а на инвертирующий – заводится цепь ОС. Меняя соотношение и , получаем требуемую глубину ОС. Выведем выражение для . Т.к. ОУ – идеальный (см. примечание выше), то: ; . Значит . Ток ОС не идёт на вход ОУ, то есть: . По закону Ома: ; . Т.к. , то решая эти уравнения совместно получим: 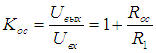. Если положить , то получим предыдущую схему. Т.к. сигнал подаётся на неинвертирующий вход, то фаза напряжения на выходе совпадает с фазой на входе.

3. Инвертирующий усилитель.

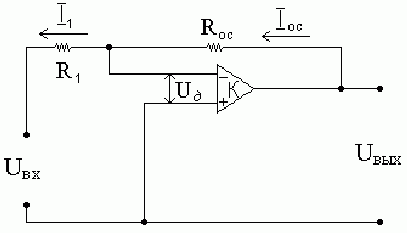
, т.к. ОУ – идеальный. По закону Ома:

.

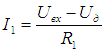
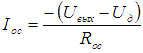Получим: .

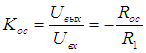ООС – параллельная по входу, на выходе сигнал инвертируется.

4. Усилитель с дифференциальным входом.

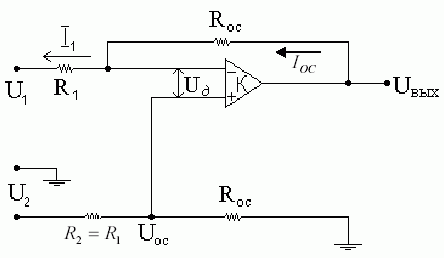
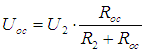
и равны по величине, разность фаз .

Такие напряжения можно получить, например, от трансформатора:

По закону Ома: , 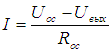. Т.к. и, учитывая, что получим: 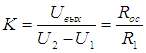. Такая схема не чувствительна к наводкам внешних магнитных полей.

5. Схема усилителя сигналов мостовой схемы.

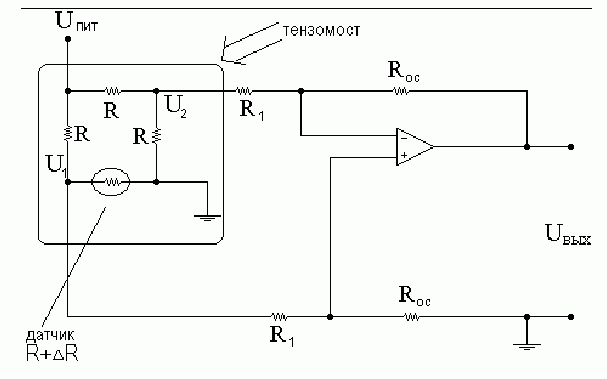
Тензодатчик:

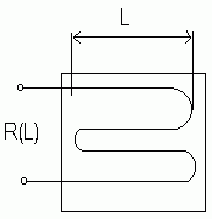
– тензодатчик. Представляет собой проволоку наклеенную на бумагу. При растягивании изменяется . В диагонали появляется напряжение разбалансирования моста.

6. Преобразователь ток – напряжение.

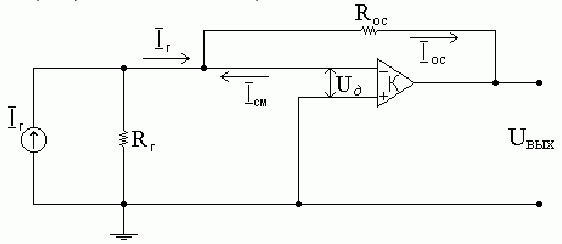
Анализируя эту схему, и принимая ОУ – идеальным, а также, полагая легко получить: . Такие схемы используются в пультах дистанционного управления.

7. Инвертирующий сумматор.

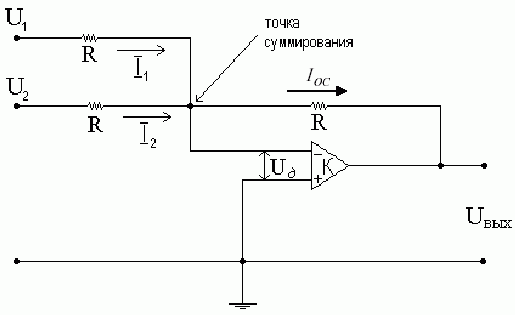
Сопротивление, на котором происходит суммирование сигналов – есть входное сопротивление ОУ с параллельной ООС через сопротивление . Из схемы, с учётом примечания очевидны следующие соотношения:

; ; ; . Отсюда: .

8. Схема суммирования с масштабными коэффициентами

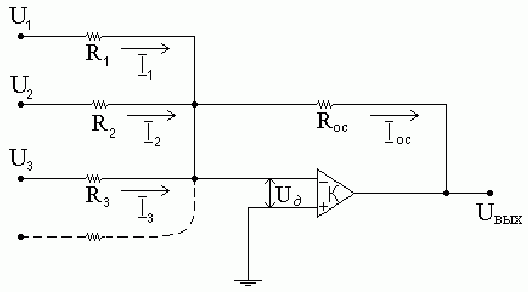
Пусть дано уравнение: . Анализируя схему установим, что коэффициенты усиления должны бать: , , . Тогда: 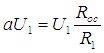, , 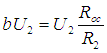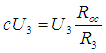. Отсюда получаем формулы для расчёта , , и т.д. задавшись ; , , .

9. Неинвертирующий сумматор.

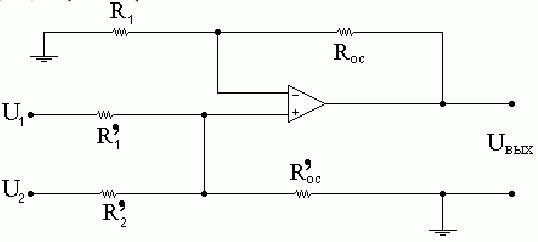
Сигнал для суммирования подаётся на неинвертирующий вход (+). Суммирование происходит на . Очевидно, для этой схемы: , если , то: , где – число входов; , если .

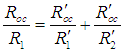10. Интегратор.

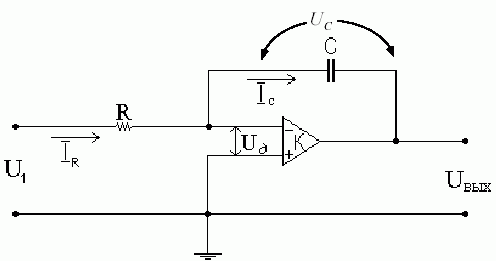
заводится через , в цепи ОС ставится ёмкость. Т.к. ОУ – идеальный (см. примечание), то . Из физики известно, что: 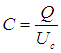, . Ток определяется как: . . Т.к. ( ), то . Откуда: . Интегрируя обе части получим: .

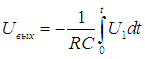11. Дифференциатор.

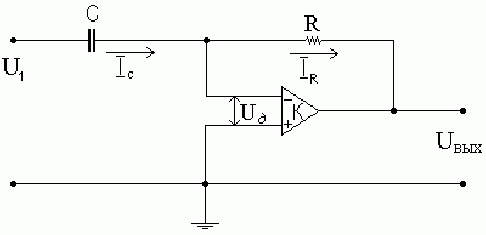
Получается из схемы интегратора путём замены и (местами).

. Т.к. , то . Таким образом, пропорционально дифференциалу . Поэтому схема называется дифференциатором. Интегрирующая и дифференцирующая цепочки имеют вид:

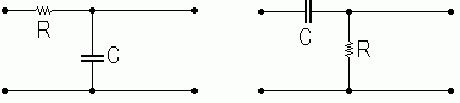
Именно включение ОУ в эти цепочки позволяет делать очень большим для интегратора, очень малым для дифференциатора и усилить сигнал.