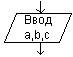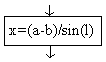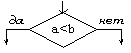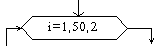Требования, предъявляемые к алгоритму

Первое правило – при построении алгоритма прежде всего необходимо задать множество объектов, с которыми будет работать алгоритм. Формализованное (закодированное) представление этих объектов носит название данных. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные. Это правило позволяет сразу отделить алгоритмы от “методов” и “способов”. Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.

Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма. Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной. В теории алгоритмов размеры памяти не ограничиваются, т. е. считается, что мы можем предоставить алгоритму любой необходимый для работы объем памяти. В школьной “теории алгоритмов” эти два правила не рассматриваются. В то же время практическая работа с алгоритмами (программирование) начинается именно с реализации этих правил.

В языках программирования распределение памяти осуществляется декларативными операторами (операторами описания переменных). В языке Бейсик не все переменные описываются, обычно описываются только массивы. Но все равно при запуске программы транслятор языка анализирует все идентификаторы в тексте программы и отводит память под соответствующие переменные.

Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно.

Четвертое правило – детерменированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки. Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.

На практике наиболее распространены следующие формы представления алгоритмов:

словесная (запись на естественном языке);

графическая (изображения из графических символов);

псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);

программная (тексты на языках программирования).

Что такое словесный способ записи алгоритмов? Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке. Например. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида). Алгоритм может быть следующим:

• задать два числа;

• если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;

• определить большее из чисел;

• заменить большее из чисел разностью большего и меньшего из чисел;

• повторить алгоритм с шага 2.

Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75. Словесный способ не имеет широкого распространения, так как такие описания: строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний. Что такое графический способ записи алгоритмов? При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление называется блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура называемых блоками. Блоки соединяются линиями переходов (называемых ветвью алгоритма), определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые блоки.

Название блока	Графическое изображение	Оприсание
Блок начало и конца алгоритма		Любой алгоритм начинается и заканчивается данным блокрм.
Блок ввода - вывода		Внутри данного блока записываются именна данных которые вводятся или выводятся в процессе выполнения алгоритма.
Блок обработки (арифметический блок)		Внури блока записываются формулы, указывающие на обработку данных.
Логический блок		Внутри блока записывается проверяемое условие, если оно истино, то выполнение алгоритма продолжается по положительной ветви, а иначе по отрицательной ветви алгоритма.
Блок начало цикла		Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Что такое псевдокод? Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой строны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. Примером псевдокода является школьный алгоритмический язык в русской нотации (школьный АЯ), описанный в учебнике А.Г. Кушниренко и др. "Основы информатики и вычислительной техники", 1991. Этот язык в дальнейшем мы будем называть просто "алгоритмический язык". Пример записи алгоритма на школьном АЯ алг Сумма квадратов (арг цел n, рез цел S)       дано | n > 0       надо | S = 1*1 + 2*2 + 3*3 + ... + n*n нач цел i       ввод n; S:=0 нц для i от 1 до n      S:=S+i*i кц вывод "S = ", S кон

31.

Процесс решения задач на компьютере – это совместная деятельность человека и ЭВМ. Этот процесс можно представить виде нескольких последовательных этапов. На долю человека приходятся этапы, связанные с творческой деятельностью – постановкой, алгоритмизацией, программированием задач анализом результатов, а на долю компьютера - этапы обработки информации с соответствии с разработанным алгоритмом.   Первый этап – постановка задачи. На этом этапе участвует человек, хорошо представляющий предметную область задачи. Он должен чётко определить цель задачи, дать словесное описание содержания задачи  и предложить общий подход к её решению. Для вычисления суммы двух целых чисел человек, знающий, как складываются числа, может описать задачу следующим образом: ввести два целых числа, сложить их и вывести сумму в качестве результата решения задачи. Второй этап – математическое и информационное моделирование. Цель этого этапа – создать такую математическую модель решаемой задачи, которая может быть реализована в компьютере. Существует целый ряд задач, где математическая постановка сводится к простому перечислению формул и логических условий. Этот этап тесно связан с первым этапом, и его можно отдельно не рассматривать, однако возможно, что для полученной модели известны несколько методов решения, и тогда предстоит выбрать лучший. Для вышеописанной задачи данный этап сведётся к следующему: введённые в компьютер числа  запомним в памяти под именами А и В, затем вычислим значение этих чисел по формуле А+В, и результат запомним в памяти под именем Summa. Третий этап – алгоритмизация задачи. На основе математического описания необходимо разработать алгоритм решения.  Четвёртый этап – программирование. Программой называется план действий, подлежащий выполнению некоторым исполнителем, в качестве которого может выступать компьютер. Составление программы обеспечивает возможность выполнение алгоритма и соответственно поставленной задачи  исполнителем – компьютером. Во многих задачах при программирование на алгоритмическом языке часто пользуются заменой блока алгоритма на один или несколько операторов, введением новых блоков, замена одних блоков на другими. Пятый этап – ввод программы и исходных данных в ЭВМ. Программа и исходные данные вводятся в ЭВМ с клавиатуры с помощью редакторов текстов, и для постоянного хранения осуществляется их запись на гибкий или жёсткий магнитный диск. Шестой этап – тестирование и отладка программы. На этом этапе происходит исполнение алгоритма с помощью ЭВМ, поиск и исключение ошибок. При этом программисту приходится выполнять рутинную работу по проверке работы программы, поиску и исключению ошибок, и поэтому для сложных программ этот этап часто требует гораздо больше времени и сил, чем написание первоначального текста программы. Отладка программы – сложный и нестандартный процесс. Исходный план отладки заключается в том, чтобы оттестировать программу на контрольных примерах.          Контрольные примеры стремятся выбрать так, чтобы при работе с ними программа прошла все основные пути блок – схемы алгоритма, поскольку на каждом из путей могут быть свои ошибки, а детализация плана зависит от того, как поведёт себя программа на этих примерах: на одном может зациклиться (т.е. бесконечно повторять одно и то же действие); на другом – дать явно неверный или бессмысленный результат и т.д. Сложные программы отлаживаются отдельными фрагментами. Для повышения качества выполнения этого этапа используются специальные программы – отладчики, которые позволяют исполнить программу “по шагам” с наблюдением за изменением значений переменных, выражений и других объектов программы, с отслеживанием выполняемых операторов. Седьмой этап – исполнение отлаженной программы и анализ результатов. На этом этапе программист запускает программу и задаёт исходные данные, требуемые по условию задачи.           Полученные в результате решения выходные данные анализируются постановщиком задачи, и на основе этого анализа вырабатываются соответствующие решения, рекомендации, выводы. Например, если при решение задачи на компьютере результат сложения двух чисел 2 и 3 будет 4, то следует сделать вывод о том, что надо изменить алгоритм и программу.          Возможно, что по итогам анализа результатов потребуется пересмотр самого подхода к решению задачи и возврат к первому этапу для повторного выполнения всех этапов с учётом приобретённого опыта. Таким образом, в процессе создания программы некоторые этапы будут повторяться до тех пор, пока мы получи алгоритм и программу, удовлетворяющие показанным выше свойствам.

32.