Задача № 8.

Определить доверительный интервал для оценки с надежностью неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если известно выборочное среднее , объем выборки n и генеральное среднее квадратическое отклонение . (См. исходные данные в таблице).

Примеры решения задач к контрольной работе №7

Пример 1. Исследовать сходимость числового ряда

.

Решение. Имеем u_n = , u_n+1 = . Применяя признак Даламбера, вычислим

l = = = = = 0 < 1.

По признаку Даламбера данный ряд сходится.

Пример 2. Исследовать сходимость числового ряда

.

Решение. Введем функцию f (x) = , удовлетворяющую условиям и исследуем сходимость, используя интегральный признак. Для этого вычислим

= = =

= = - = .

Несобственный интеграл сходится, следовательно, сходится и данный ряд

Пример 3. Найти интервал сходимости степенного ряда

.

Решение. Составим ряд из модулей членов данного ряда и вычислим l = =

= = .

По признаку Даламбера ряд сходится при l < 1, отсюда

< 1 или |x| < 3. Следовательно, ряд абсолютно сходится при x (-3,3). Исследуем сходимость ряда в граничных точках. При x =3 и x = -3 из данного ряда получаем соответственно числовые ряды и ^. Из интегрального признака сходимости следует, что эти ряды сходятся абсолютно, поэтому интервалом сходимости данного ряда является промежуток [-3,3].

Пример 4. Вычислить определенный интеграл

cos dx

с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.

Решение. Пользуясь рядом Маклорена для cos x, заменяя в нем x на , имеем

cos =1 – + – + – ... (x 0). Интегрируя в указанных пределах , получим

cos dx = x – + – + … = 1– + – + …

Четвертый член этого знакочередующегося сходящегося ряда меньше 0,001. Поэтому для вычисления искомого приближенного значения интеграла достаточно взять три первых члена ряда:

cos dx = 1– 1/4 + 1/72 = 0,764.

Пример 5. Разложить функцию f (x) = + x в ряд Фурье в интервале (- , ).

Решение. Функция удовлетворяет условиям теоремы о сходимости, следовательно ее можно разложить в ряд Фурье.

Определяем коэффициенты ряда Фурье

a₀ = f (x) dx = ( + x ) dx = dx + x dx.

Второй интеграл равен нулю как интеграл от нечетной функции, взятый по интервалу, симметричному относительно начала координат. Поэтому a₀ = dx = 2 . Аналогично,

= f (x) cosmx dx = ( +x) cosmx dx =

= cos mx dx + x cosmx dx=0.

Далее, = f (x) sin mx dx = ( +x) sin mx dx =

= sin mx dx + x sin mx dx.

Первый интеграл равен нулю. Подынтегральная функция второго интеграла четная, т.к. является произведением двух нечетных функций. Таким образом,

= x sin mx dx = =

= - cos mx + cos mx dx = - cos m +

+ sin mx = - ( -1) = .

Разложение функции f (x) в ряд Фурье имеет вид

f (x) = + 2 sin mx = +2 sin 2x +

+ sin 3x – .

Пример 6. Разложить функцию f (x) = в ряд Фурье.

Решение. График периодического продолжения заданной функции на всю числовую ось с периодом 2 l = 4 имеет вид, изображенный на рис.3.

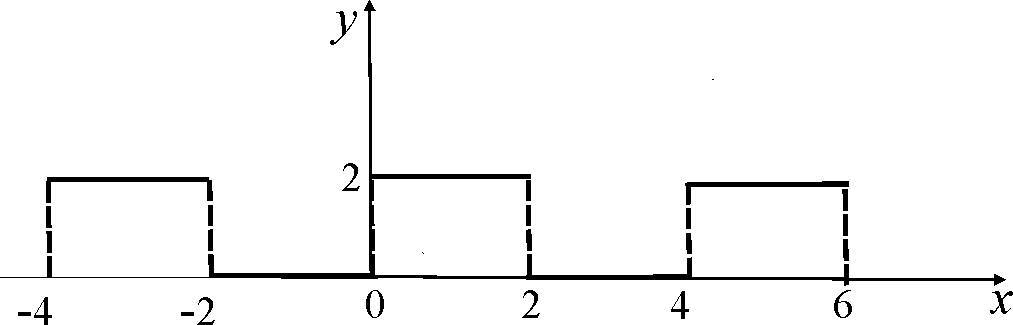
Рис. 1.

Определяем коэффициенты ряда Фурье

a₀ = f (x) dx = f (x) dx =

= = x =2,

= f (x) cos dx = 2 cos dx =

= sin = (sin n - sin 0) = 0,

= f (x) sin dx = 2sin dx =

= cos = (- cos n + 1) = [( -1) + 1]=

=

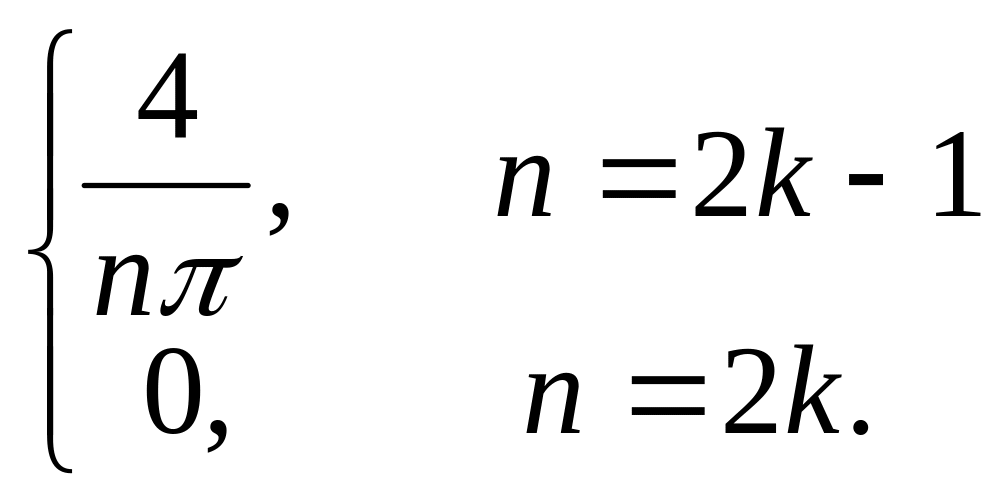
Получаем ряд Фурье

f (x) = 1 + + sin +... + .

Пример 7. Найти изображение по Лапласу функции

f (x)= cos 4t sin 2t.

Решение. Предварительно преобразуем исходную функцию, воспользовавшись формулой

sin ax cos bx = ( sin (a+b) + sin (a -b)),

будем иметь f (x) = (sin 6t - sin 2t). Зная изображения функций sin 6t и sin 2t , по теореме смещения получим

sin 6t ; sin 2t .

Используя свойство линейности изображений Лапласа, окончательно запишем

f (x) = sin 6t - sin 2t

- .

Пример 8. Найти функцию-оригинал для функции

F (p)= .

Решение. Для отыскания функции-оригинала по данному изображению разложим функцию F (p) на простейшие дроби

F (p) = = + + .

Неизвестные А, В, С и D находим методом неопределенных коэффициентов. Для этого приводим правую часть равенства к общему знаменателю

= .

Из тождественного равенства дробей заключаем, что коэффициенты при соответствующих степенях р в числителях дробей слева и справа от знака равенства должны быть равны. Это приводит к следующей системе уравнений для коэффициентов А, В, С, D

А + С = 0 Откуда получаем

В + D = 0 A = 0, B = 1/4,

4A =0 C =0, D = -1/4.

4B = 1.

Поэтому = - .

Для каждой из полученных дробей с помощью таблицы изображений основных элементарных функций легко установить функцию-оригинал

t; = sin 2t.

Откуда F (p) = t - sin 2t.

Пример 9. Методом операционного исчисления найти решение дифференциального уравнения с начальными условиями х(0) = 0, 1.

Решение. Пусть решение x (t) имеет изображение (p),

x (t) ¸ (p). Тогда по теореме о дифференцировании оригинала получим (t) ¸ p (p) - x(0); (t) ¸ p² (p) - p x(0)- (0).

Запишем изображение правой части исходного уравнения ¸ , тогда заданное дифференциальное уравнение примет вид

(p² (p) - 1) - 3 ( p (p) - 0) - 4 (p) =

или (p) (p²- 3 p - 4) = 1+ .

Поэтому (p) = .

Функция (p) является изображением решения исходной задачи. Найдем функцию-оригинал x(t). Для этого разложим дробь на простейшие

= = + + .

Методом неопределенных коэффициентов получим А=1/5, B=4/25, C=-4/25.

Для полученных дробей найдем функции-оригиналы

¸ t ; ¸ ; ¸ .

Окончательно решение дифференциального уравнения запишется в виде

x (t) = + - .

Пример 10. Найти решения системы уравнений

удовлетворяющие начальным условиям x(0) = y(0) = 0.

Решение. Обозначим x (t) ¸ x(p) , y (t) ¸` (p) и напишем систему вспомогательных уравнений

(3p + 2) (p) + p (p) = 1/p, p (p) +(4 p +3) (p) = 0.

Решая эту систему, находим

(p) = = - - ,

(p) = - = = .

Здесь правые части уравнений разложены на простейшие дроби, как показано в примере 8 . По изображениям находим функции-оригиналы, т.е. искомые решения системы

x(t) = - - ,

у(t) = ( - ).