
- •Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее, частное и особое решения.
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.
- •Линейные уравнения первого порядка
- •Метод вариации произвольной постоянной (метод Лагранжа).
- •Метод и.Бернулли.
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения, допускающие понижение порядка
- •Учитывая, что ,
- •Искомое частное решение имеет вид
- •Линейные дифференциальные уравнения высших порядков
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Линейные дифференциальные уравнения высших порядков
Опр.
Линейным дифференциальным уравнением
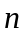 -го
порядка называется
уравнение вида
-го
порядка называется
уравнение вида
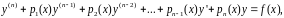 (31)
(31)
где
 - искомая функция аргумента
,
а функции
- искомая функция аргумента
,
а функции
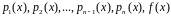 заданы и непрерывны на некотором
промежутке
заданы и непрерывны на некотором
промежутке
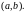
Если всюду в
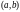 функция
функция
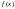 тождественно равна нулю, то уравнение
(31) называется линейным
однородным, в противном
случае – линейным
неоднородным.
тождественно равна нулю, то уравнение
(31) называется линейным
однородным, в противном
случае – линейным
неоднородным.
Рассмотрим линейное
однородное дифференциальное уравнение
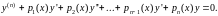 (32)
(32)
Отметим его свойства:
1. Если функция
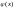 является решением уравнения (32), а
- любая постоянная, то и функция
является решением уравнения (32), а
- любая постоянная, то и функция
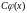 есть также решение уравнения (32).
есть также решение уравнения (32).
2. Если функции
 являются решениями уравнения (32), то и
их сумма
являются решениями уравнения (32), то и
их сумма
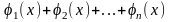 также является решением уравнения (32).
также является решением уравнения (32).
3. Если функции являются решениями однородного уравнения (32), то их линейная комбинация
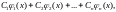 где
где
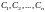 - произвольные постоянные, также является
решением этого уравнения.
- произвольные постоянные, также является
решением этого уравнения.
Опр.
Функции
 ,
определенные и непрерывные на интервале
,
определенные и непрерывные на интервале
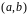 ,
называются линейно
зависимыми на
,
называются линейно
зависимыми на
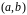 ,
если существует такой набор чисел
,
если существует такой набор чисел
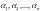 ,
среди которых хотя бы одно отлично от
нуля, что при любом
,
среди которых хотя бы одно отлично от
нуля, что при любом
 на интервале
на интервале
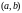 выполняется тождество
выполняется тождество

Если же это тождество
выполнено только при условии
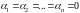 ,
то функции называют линейно
независимыми на интервале
,
то функции называют линейно
независимыми на интервале
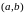 .
.
Видно, что если функции
 линейно зависимы на
линейно зависимы на
 ,
то, по крайней мере, одну из них можно
выразить в виде линейной комбинации
остальных. Например,
,
то, по крайней мере, одну из них можно
выразить в виде линейной комбинации
остальных. Например,
 если
если
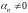 .
.
Пусть функции
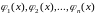 дифференцируемы
дифференцируемы
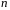 раз на интервале
раз на интервале
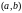 .
Рассмотрим определитель
-го
порядка
.
Рассмотрим определитель
-го
порядка

который называют определителем
Вронского (вронскианом) для
рассматриваемых функций. Он является
функцией от
,
определенной на интервале
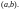
Теорема
(признак линейной независимости решений
линейного однородного уравнения).
Для того, чтобы
решений
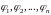 уравнения (32) были линейно независимы
на
уравнения (32) были линейно независимы
на
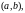 необходимо и достаточно, чтобы определитель
Вронского для этих решений не обращался
в нуль ни в одной точке из
необходимо и достаточно, чтобы определитель
Вронского для этих решений не обращался
в нуль ни в одной точке из
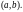
Использование этого признака облегчается наличием двух важных свойств:
1. Если определитель Вронского
для этих решений обращается в нуль в
одной точке интервала
,
то он равен нулю во всех точках
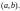
2. Если определитель Вронского
для этих решений не равен нулю в одной
точке интервала
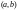 ,
то он отличен от нуля во всех точках
,
то он отличен от нуля во всех точках
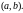
Опр.
Фундаментальной системой решений
линейного однородного уравнения
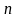 -го
порядка на интервале
-го
порядка на интервале
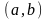 называется любая система из
решений этого уравнения, линейно
независимых на
.
называется любая система из
решений этого уравнения, линейно
независимых на
.
Теорема
(о структуре общего решения однородного
линейного уравнения).
Если
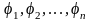 - фундаментальная система решений
уравнения (32) на интервале
,
то линейная комбинация этих решений
- фундаментальная система решений
уравнения (32) на интервале
,
то линейная комбинация этих решений
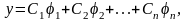
где
 - произвольные постоянные, является
общим решением уравнения (32) в области
- произвольные постоянные, является
общим решением уравнения (32) в области
 Обратимся к рассмотрению линейных
неоднородных дифференциальных уравнений
вида (31)
Обратимся к рассмотрению линейных
неоднородных дифференциальных уравнений
вида (31)
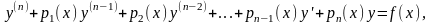
где
 - искомая функция аргумента
,
а функции
- искомая функция аргумента
,
а функции
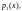
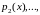
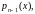
 заданы и непрерывны на некотором
интервале
.
заданы и непрерывны на некотором
интервале
.
Если в уравнении (31) сохранить левую часть, а в правой функцию f(x) заменить нулем, то получим так называемое однородное уравнение, соответствующее неоднородному уравнению (31).
Теорема (о структуре общего решения неоднородного линейного уравнения). Общее решение линейного неоднородного уравнения (31) в области
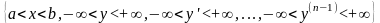
есть сумма любого его частного решения и общего решения соответствующего однородного уравнения в указанной области, т.е.
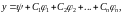 (33)
(33)
где
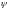 - частное решение уравнения (31),
- частное решение уравнения (31),
 - фундаментальная система решений
однородного уравнения (32), а
-
произвольные постоянные
- фундаментальная система решений
однородного уравнения (32), а
-
произвольные постоянные
Теорема
(принцип наложения решений). Если
на промежутке
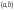 функция
функция
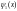 - частное решение уравнения
- частное решение уравнения
 а функция
а функция
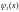 - частное решение уравнения
- частное решение уравнения
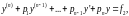
то на этом же промежутке
функция
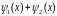 есть частное решение уравнения
есть частное решение уравнения
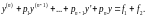
Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Рассмотрим уравнение второго
порядка
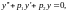 (39)
где
(39)
где
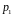 и
и
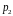 - любые вещественные числа.
- любые вещественные числа.
Л.Эйлер предложил искать
частные решения этого уравнения в виде
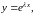 где
где
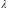 -
некоторое число.
-
некоторое число.
Подставим

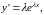
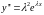 в левую часть уравнения и получим
в левую часть уравнения и получим
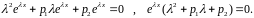
Множитель
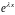 отличен от нуля, следовательно, число
отличен от нуля, следовательно, число
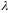 должно быть корнем уравнения
должно быть корнем уравнения
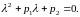 (40)
(40)
Это уравнение называется характеристическим уравнением уравнения (39), а его корни - характеристическими числами уравнения (39).
Уравнение (40) квадратное и
имеет два корня
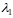 и
и
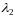 .
.
Структура фундаментальной системы решений зависит от вида корней характеристического уравнения. Рассмотрим три возможных случая:
1) Пусть
 - вещественные и различные. Тогда частные
решения уравнения запишутся так:
- вещественные и различные. Тогда частные
решения уравнения запишутся так:
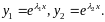
Найдем определитель Вронского
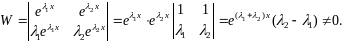
Эти решения линейно независимы и образуют фундаментальную систему решений уравнения (39), следовательно, его общее решение можно записать в виде
 где
где
 и
и
 - произвольные
постоянные.
- произвольные
постоянные.
2)
Пусть
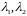 - вещественные и равные.
- вещественные и равные.
В этом случае дискриминант
квадратного уравнения равен нулю и
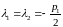 .
Одно решение получается на основании
предыдущих рассуждений: это функция
.
Одно решение получается на основании
предыдущих рассуждений: это функция
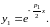 Подстановкой
можно убедиться в том, что функция
Подстановкой
можно убедиться в том, что функция
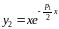 является решением уравнения (40) и линейно
независима с решением
является решением уравнения (40) и линейно
независима с решением
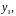 следовательно, общее решение уравнения
(39) имеет вид
следовательно, общее решение уравнения
(39) имеет вид
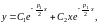 где
где
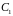 и
и
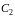 - произвольные
постоянные.
- произвольные
постоянные.
3) Пусть
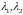 - комплексные корни. Так как числа
- комплексные корни. Так как числа
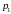 и
и
 вещественные, то
вещественные, то
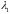 и
и
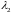 являются сопряженными.
являются сопряженными.
Можно показать, что паре комплексных сопряженных корней
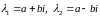
соответствует два
линейно независимых
частных решения
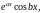
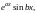
и, следовательно, общее решение уравнения (39) в этом случае имеет вид
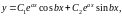 где
где
 и
и
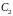 - произвольные постоянные.
- произвольные постоянные.
Примеры. Найти общее решение для уравнений
1)
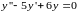 .
.
Данное уравнение является
линейным однородным дифференциальным
уравнением второго порядка с постоянными
коэффициентами. Составим характеристическое
уравнение для него:

Найдем корни характеристического
уравнения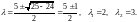
Общее решение будет иметь
вид
 где
где
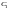 и
и
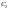 - произвольные
постоянные.
2)
- произвольные
постоянные.
2)
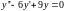 .
.
Составим характеристическое
уравнение: .
.
Найдем его корни
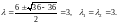
Общее решение будет иметь
вид
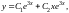 где
где
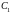 и
и
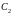 - произвольные
постоянные.
- произвольные
постоянные.
3)
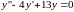 .
.
Составим характеристическое
уравнение
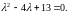
Найдем его корни
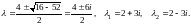
Запишем общее решение
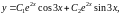 где
где
 и
- произвольные
постоянные.
и
- произвольные
постоянные.
