
- •Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее, частное и особое решения.
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.
- •Линейные уравнения первого порядка
- •Метод вариации произвольной постоянной (метод Лагранжа).
- •Метод и.Бернулли.
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения, допускающие понижение порядка
- •Учитывая, что ,
- •Искомое частное решение имеет вид
- •Линейные дифференциальные уравнения высших порядков
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Общее, частное и особое решения.
Если закрепить начальное
значение абсциссы
 ,
а начальному значению
,
а начальному значению
 придавать различные допустимые значения
придавать различные допустимые значения
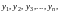 то каждому такому значению будет
соответствовать единственная интегральная
кривая, и в области
то каждому такому значению будет
соответствовать единственная интегральная
кривая, и в области
 множество всех интегральных кривых
образует семейство кривых, зависящих
от одного параметра, который может
изменяться в определенных пределах и
который принято обозначать через
множество всех интегральных кривых
образует семейство кривых, зависящих
от одного параметра, который может
изменяться в определенных пределах и
который принято обозначать через
 ,
так что все семейство интегральных
кривых может быть описано уравнением
,
так что все семейство интегральных
кривых может быть описано уравнением
 (4)
(4)
Опр.
Функция
 ,
непрерывно дифференцируемая по
,
непрерывно дифференцируемая по
 ,
называется общим
решением уравнения
,
называется общим
решением уравнения
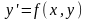 в области
,
если она удовлетворяет следующим
условиям:
в области
,
если она удовлетворяет следующим
условиям:
1) равенство
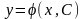 разрешимо в области
относительно произвольной постоянной:
разрешимо в области
относительно произвольной постоянной:
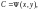
2) функция
 является решением уравнения
для всякого значения постоянной
является решением уравнения
для всякого значения постоянной
 ,
полученной выше, где точка
,
полученной выше, где точка
 - любая точка из области
.
- любая точка из области
.
Чтобы решить задачу Коши
для любых начальных значений
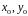 из области
,
надо заменить в формуле (4) переменные
из области
,
надо заменить в формуле (4) переменные
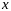 и
и
 числами
числами
 и
и
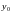 ,
решить полученное уравнение
,
решить полученное уравнение
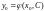 относительно
относительно
 ,
т.е. получить соотношение
,
т.е. получить соотношение
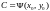 ,
и подставить найденное значение в общее
решение
.
Полученная функция
,
и подставить найденное значение в общее
решение
.
Полученная функция
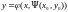 и есть искомое решение.
и есть искомое решение.
Опр.
Общее решение уравнения
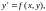 записанное в виде, не разрешенном
относительно искомой функции, т.е. в
виде
записанное в виде, не разрешенном
относительно искомой функции, т.е. в
виде
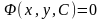 или
или
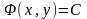 ,
называют общим
интегралом этого уравнения.
,
называют общим
интегралом этого уравнения.
Решение, которое получается
из общего решения
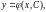 если в нем произвольной постоянной
если в нем произвольной постоянной
 придать конкретное значение, называется
частным решением.
придать конкретное значение, называется
частным решением.
Решение, которое не может быть получено из общего решения (общего интеграла) ни при каком конкретном значении произвольной постоянной, называется особым решением. Геометрически ему соответствует интегральная кривая, не содержащаяся в семействе интегральных кривых, составляющих общее решение. Через каждую точку такой интегральной кривой проходит, по крайней мере, еще одна интегральная кривая из общего решения того же уравнения, имеющая в этой точке ту же касательную.
Пример.
Рассмотрим уравнение
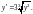
Т.к. правая часть этого
уравнения и ее частная производная
удовлетворяют условиям теоремы во
всех точках плоскости
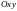 за исключением точек оси
за исключением точек оси
 ,
то через любую точку
,
то через любую точку
 при
при
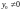 проходит единственная интегральная
кривая данного уравнения. Т.к.
проходит единственная интегральная
кривая данного уравнения. Т.к.
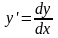 ,
то
,
то
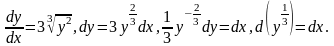
В левой части равенства
стоит дифференциал функции
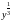 ,
а в правой - дифференциал функции
,
а в правой - дифференциал функции
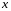 .
Дифференциалы функций равны, значит,
сами функции отличаются на константу
.
Дифференциалы функций равны, значит,
сами функции отличаются на константу
 ,
тогда
,
тогда
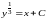 или
или
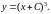
Найденная функция является
общим решением заданного уравнения
всюду на плоскости
 за исключением оси
за исключением оси
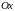 .
Рассмотрим точки оси Ох.
Подставим функцию
.
Рассмотрим точки оси Ох.
Подставим функцию
 в уравнение
в уравнение
 Получим тождество, т.е.
Получим тождество, т.е.
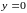 является решением данного уравнения.
Это решение является особым, т.к. не
может быть получено из общего решения
является решением данного уравнения.
Это решение является особым, т.к. не
может быть получено из общего решения
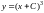 ни при каком значении постоянной
.
ни при каком значении постоянной
.
З

 оси
оси
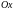 проходит кривая
проходит кривая
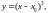 совпадающая при
совпадающая при
 с общим решением, касательной к которой
в этой точке является сама ось
с общим решением, касательной к которой
в этой точке является сама ось

