Дифференциальные уравнения высших порядков

Дифференциальное уравнение -го порядка с одной неизвестной функцией у аргумента всегда можно записать в виде

где 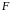означает известную функцию своих аргументов, причем производная обязательно содержится в уравнении.

Решением дифференциального уравнения -го порядка на промежутке называется всякая функция

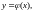
которая определена и раз дифференцируема на этом промежутке и которая при подстановке в уравнение обращает его в тождество на промежутке .

Дифференциальные уравнения, допускающие понижение порядка

Первый тип - это уравнение вида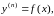 (26) где - функция, непрерывная на некотором промежутке . Т.к.

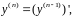
то уравнение (26) можно записать в виде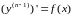

откуда следует 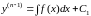. (27)

Учитывая, что ,

проинтегрируем (27) и получим 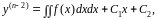где C₁ и C₂ - постоянные.

Так получим общее решение данного уравнения в области

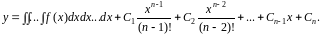
Пример. Найти решение уравнения

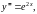
удовлетворяющее начальным условиям

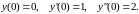
Это уравнение рассмотренного типа. Т.к. функция непрерывна на всей оси , то общее решение может быть получено после трехкратного последовательного интегрирования функции 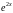, а именно

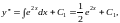
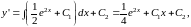
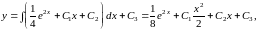где 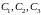- произвольные постоянные.

Для получения частного решения, удовлетворяющего начальным условиям, подставим в полученные выражения соответствующие начальные значения:

, откуда

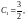
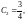
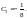
Искомое частное решение имеет вид

Второй тип - это уравнение вида (28)

где - заданная функция своих аргументов, а натуральное число 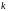удовлетворяет неравенству 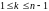, т.е. это тип уравнения, не содержащего искомой функции и ее производных до порядка 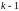включительно.

Введем новую неизвестную функцию 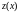, положив 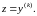(29)

Тогда

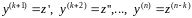
и уравнение (28) принимает вид

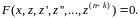
Это дифференциальное уравнение порядка 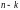относительно неизвестной функции 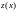, то есть порядок понижается на 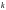единиц.

Пример. Решить уравнение 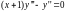, считая, что .

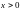Данное уравнение не содержит неизвестной функции и ее производной вводим подстановку

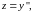
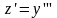
и получаем уравнение первого порядка:

Это уравнение с разделяющимися переменными, поэтому ,

,

.

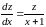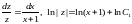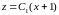Вернемся к переменной y:

получим дифференциальное уравнение второго порядка первого типа.

Выполняя последовательно двукратное интегрирование функции , получим общее решение данного уравнения

где С_1, и 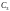- произвольные постоянные.

Третий тип - это уравнение вида (30)

где 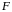- заданная функция своих аргументов, т.е. это тип уравнений, не содержащих явно независимой переменной. Порядок уравнения этого типа может быть понижен на единицу. Введем подстановку

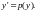
В согласии с правилом дифференцирования сложной функции будем иметь

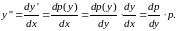
Используя полученное выражение, имеем

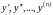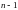Заменяя в уравнении (30) производные полученными выражениями, запишем дифференциальное уравнение порядка относительно новой неизвестной функции аргумента 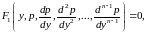где 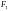- известная функция своих аргументов.

Пример. Решить уравнение

Данное уравнение имеет второй порядок и не содержит явно независимой переменной и поэтому относится к третьему типу. Если ввести подстановку 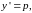считая функцией , то

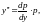
а тогда данное уравнение можно записать в виде .

Это дифференциальное уравнение распадается на два:

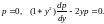
Первое из них дает 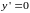, т.е. 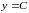, где =const

Разделим переменные во втором уравнении и проинтегрируем его:

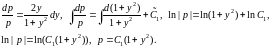
Т.к. 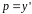, то

, откуда (*)

При 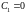решение первого уравнения содержится в выражении (*). Значит, (*) представляет собою общий интеграл данного в условии уравнения.