
- •Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее, частное и особое решения.
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.
- •Линейные уравнения первого порядка
- •Метод вариации произвольной постоянной (метод Лагранжа).
- •Метод и.Бернулли.
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения, допускающие понижение порядка
- •Учитывая, что ,
- •Искомое частное решение имеет вид
- •Линейные дифференциальные уравнения высших порядков
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Уравнения с разделяющимися переменными
О
пр. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если правая часть его представляется в виде произведения функции, зависящей только от аргумента , на функцию, зависящую только от искомой функции
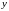 .
Его можно записать в виде
.
Его можно записать в виде
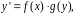 (5)
(5)
где функция
 определена и непрерывна на интервале
определена и непрерывна на интервале
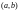 ,
а функция
,
а функция
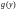 определена, имеет непрерывную производную
и не обращается в нуль на интервале
определена, имеет непрерывную производную
и не обращается в нуль на интервале
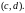
Умножив обе части рассмотренного
уравнения на
 и разделив на
и разделив на
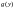 ,
получим
,
получим

где в левой части находится
функция от
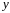 и
и
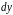 ,
а в правой - функция от
и
,
а в правой - функция от
и
 .
.
Проинтегрируем обе части
тождества
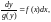 помня, что первообразные отличаются
друг от друга на константу, и получим
помня, что первообразные отличаются
друг от друга на константу, и получим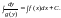 (6)
(6)
Это общий интеграл уравнения
с разделяющимися переменными в
прямоугольнике
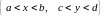 .
.
Пусть теперь функция
 обращается в нуль при некотором
обращается в нуль при некотором
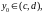 так что
так что
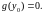 Подставим
Подставим
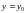 в уравнение
в уравнение
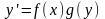 и заметим, что оно удовлетворяется,
т.е.
и заметим, что оно удовлетворяется,
т.е.
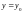 является его решением. При этом оно
не содержится в соотношении (6), а, значит,
будет являться особым решением.
является его решением. При этом оно
не содержится в соотношении (6), а, значит,
будет являться особым решением.
Пример
.
Найти решение уравнения
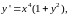
удовлетворяющее начальному
условию

Это уравнение с разделяющимися
переменными, где
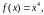 а
а
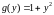 .
Функции
.
Функции
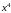 и
и
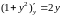 непрерывны при любых значениях
и
непрерывны при любых значениях
и
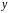 ,
причем
,
причем
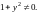 Запишем
Запишем
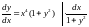 ,
, 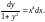
 ,
,

где
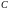 - произвольная постоянная.
- произвольная постоянная.
Для решения поставленной
задачи Коши положим в общем интеграле
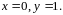
Тогда
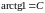 ,
,
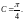
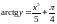 .
.
Разрешив тождество
относительно
,
получим частное решение, удовлетворяющее
заданному начальному условию:

Уравнение с разделяющимися переменными может быть задано в симметричной относительно и форме:
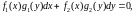 (7)
(7)
где функции
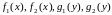 заданы и непрерывны соответственно в
интервалах
заданы и непрерывны соответственно в
интервалах
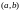 и
и
 причем
причем
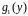 и
и
 не обращаются в нуль.
не обращаются в нуль.
Разделим обе части данного
уравнения на произведение
 и получим общий интеграл уравнения в
прямоугольнике
и получим общий интеграл уравнения в
прямоугольнике
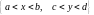
в следующем виде
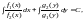 (8)
где
- произвольная постоянная.
(8)
где
- произвольная постоянная.
Пример.
Решить уравнение
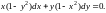
Данное дифференциальное
уравнение есть уравнение с разделяющимися
переменными. Функции
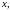
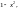
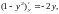
 непрерывны при любых значениях
и
,
причем будем пока считать, что
непрерывны при любых значениях
и
,
причем будем пока считать, что
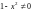 и
и
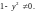
Разделив обе части данного
уравнения на произведение
 получим:
получим:

Преобразуем выражение:
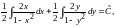
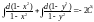
и проинтегрируем:
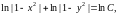
где C>0
(здесь произвольная постоянная
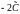 обозначена через lnC).
обозначена через lnC).
Последнее равенство можно записать в виде
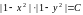 , т.е.
, т.е.
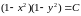 ,
где C>0
или C<0.
,
где C>0
или C<0.
Мы получили общий интеграл
данного уравнения при условиях
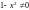 и
и

Рассмотрим теперь случай
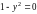 ,
т.е.
,
т.е.
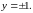 Непосредственно из уравнения
Непосредственно из уравнения
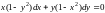
видно, что каждый из случаев
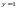 и
и
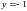 является решением. При этом они содержатся
в общем интеграле и могут быть получены
из него при
является решением. При этом они содержатся
в общем интеграле и могут быть получены
из него при
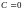 .
.
Аналогично рассматриваются
решения, доставляемые уравнением
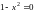 ,
т.е.
,
т.е.
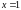 и
и
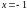 .
.
Пример.
Решить уравнение при
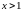 :
:

Разделим переменные.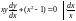
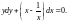
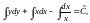
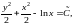
Тогда общий интеграл запишем в виде
 где
где
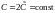 .
.
