
- •Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее, частное и особое решения.
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.
- •Линейные уравнения первого порядка
- •Метод вариации произвольной постоянной (метод Лагранжа).
- •Метод и.Бернулли.
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения, допускающие понижение порядка
- •Учитывая, что ,
- •Искомое частное решение имеет вид
- •Линейные дифференциальные уравнения высших порядков
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Дифференциальные уравнения
Опр. Дифференциальными уравнениями называют уравнения, в которых содержатся производные неизвестных функций.
Если неизвестные функции являются функциями только одного независимого переменного, то уравнения называются обыкновенными, в противном случае - дифференциальными уравнениями в частных производных. Примером дифференциального уравнения в частных производных является уравнение
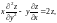
служащее для определения
функции двух переменных
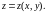 В дальнейшем мы будем рассматривать
только обыкновенные дифференциальные
уравнения.
В дальнейшем мы будем рассматривать
только обыкновенные дифференциальные
уравнения.
Опр. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Например,
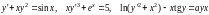 являются уравнениями первого порядка,
а
являются уравнениями первого порядка,
а 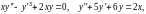 - уравнениями второго порядка.
- уравнениями второго порядка.
Любое обыкновенное
дифференциальное уравнение
 -го
порядка с одной неизвестной функцией
-го
порядка с одной неизвестной функцией
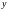 аргумента
аргумента
 можно записать в виде
можно записать в виде 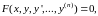 (1)
где
(1)
где
 - известная функция своих аргументов.
- известная функция своих аргументов.
Опр.
Решением дифференциального уравнения
(1) на промежутке
 называется функция
называется функция
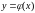 ,
,
 раз дифференцируемая на этом промежутке
и которая при подстановке ее вместо
раз дифференцируемая на этом промежутке
и которая при подстановке ее вместо
 в уравнение (1) обращает его в тождество
на всем промежутке
в уравнение (1) обращает его в тождество
на всем промежутке
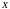 .
.
График решения
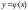 дифференциального уравнения (1) называется
интегральной кривой
этого уравнения.
дифференциального уравнения (1) называется
интегральной кривой
этого уравнения.
Процесс отыскания решений
дифференциального уравнения называется
интегрированием этого
уравнения.
Иногда решение получают
в параметрическом виде
 где
где
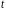 - параметр, или в неявной форме
- параметр, или в неявной форме
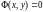 .
.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение
первого порядка
записывается в виде
 где
где
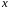 - независимая переменная,
- независимая переменная,
 - его неизвестная функция, a
- его неизвестная функция, a
 -
заданная функция трех переменных в
некоторой области пространства трех
переменных. Если это уравнение может
быть разрешено относительно производной
-
заданная функция трех переменных в
некоторой области пространства трех
переменных. Если это уравнение может
быть разрешено относительно производной
 ,
то получим уравнение вида
,
то получим уравнение вида
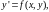 (2)
(2)
где
 - известная функция, определенная в
некоторой области
- известная функция, определенная в
некоторой области
 на плоскости
на плоскости
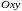 .
Уравнение (2) называют уравнением
в нормальной форме.
.
Уравнение (2) называют уравнением
в нормальной форме.
Уравнение (2) можно записать
и в виде
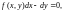 если вспомнить, что
если вспомнить, что
 .
.
Оно является частным случаем уравнения в дифференциальной форме вида
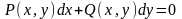 ,
где
,
где
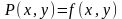 ,
,
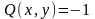 .
.
Задача Коши.
Найти решение
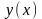 уравнения
уравнения
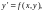 удовлетворяющее условию
удовлетворяющее условию
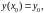 (3) где
(3) где
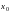 и
и
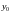 - любые числа, для которых определена
функция
- любые числа, для которых определена
функция
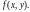 Условие (3) называют начальным
условием, числа
и
Условие (3) называют начальным
условием, числа
и
 - начальными значениями
решения уравнения (2), а саму задачу -
задачей Коши или
начальной задачей.
С геометрической точки зрения задача
Коши состоит в нахождении интегральной
кривой, проходящей через данную точку
- начальными значениями
решения уравнения (2), а саму задачу -
задачей Коши или
начальной задачей.
С геометрической точки зрения задача
Коши состоит в нахождении интегральной
кривой, проходящей через данную точку
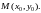
Решение задачи Коши единственно, о чем говорит следующая теорема.
Т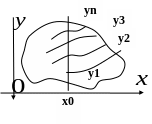 еорема.
Если в уравнении
еорема.
Если в уравнении
 функция
функция
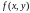 и ее частная производная
и ее частная производная
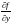 непрерывны в некоторой области
непрерывны в некоторой области
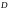 на плоскости
на плоскости
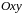 ,
то, какова бы ни была точка
,
то, какова бы ни была точка
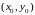 области
области
 ,
существует единственное решение
,
существует единственное решение
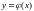 этого уравнения, определенное в некотором
интервале, содержащем точку
этого уравнения, определенное в некотором
интервале, содержащем точку
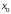 и удовлетворяющее условию
и удовлетворяющее условию
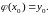 .
.
Геометрический смысл
этой теоремы состоит в том, что через
каждую точку
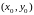 области
проходит одна и только одна интегральная
кривая указанного уравнения, т.е. вся
область
области
проходит одна и только одна интегральная
кривая указанного уравнения, т.е. вся
область
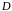 покрыта интегральными кривыми уравнения,
которые нигде не пересекаются между
собой.
покрыта интегральными кривыми уравнения,
которые нигде не пересекаются между
собой.
