3.Элементы аналитической геометрии.

6.

Угол φ между двумя плоскостями – это угол между их нормальными векторами, поэтому его можно найти, используя скалярное произведение нормальных векторов.

Если известны общие уравнения двух плоскостей

,

то можно выписать их нормальные векторы

Тогда угол φ между нормальными векторами находится по формуле:

- это угол между плоскостями.

Если плоскости параллельны, то их нормальные векторы тоже параллельны, т.е.

- условие параллельности.

Если плоскости перпендикулярны, то их нормальные векторы тоже перпендикулярны, т.е.

- условие перпендикулярности.

7.

а). Общее уравнение прямой.

- вектор.

- каноническое уравнение прямой.

Где, - координаты какого-нибудь направляющего вектора прямой, а - координаты точки, через которую проходит прямая.

б). Каноническое уравнение прямой.

Если каждое соотношение в равенстве обозначить через параметр t, то получим: Выражая x,y,z из полученных равенств,

получим систему равенств:

Параметрические уравнения прямой в пространстве.

в). Параметрические уравнения прямой.

Прямая в пространстве определяется как пересечение двух плоскостей. Пусть уравнения плоскостей имеют вид:

Эти уравнения определяют общее уравнение прямой в пространстве.

г). Уравнение прямой проходящей через две точки.

Чтобы получить уравнение прямой проходящей через две точки и , нужно в качестве направляющего вектора прямой взять вектор

Подстави

в в равенство в числителе вместо координаты точки , а в знаменателе вместо p,m,n координаты вектора , получим уравнение

- уравнение прямой проходящей через две точки.

8.

Пусть заданы канонические уравнения прямых

и

и - направляющие векторы этих прямых. Прямые параллельны, если параллельны их направляющие векторы, т.е. Из условия коллинеарности векторов следует: - условие параллельности.

Если прямые перпендикулярны, то перпендикулярны и их направляющие векторы, т.е. , а значит их скалярное произведение равно 0.

- условие перпендикулярности.

Угол между прямыми – это угол между их направляющими векторами. Его можно найти используя скалярное произведение векторов.

9.Прямая и плоскость в пространстве могут быть различно расположены по отношению друг к другу:

1.Они параллельны между собой.

В этом случае направляющий вектор прямой и нормальный вектор плоскости взаимно перпендикулярны , т.е. их скалярное произведение равно 0: .

Е сли уравнение плоскости , а уравнение прямой , то условие параллельности будет иметь вид: .

2.Они могут иметь одну общую точку, т.е. пересекаются. При этом:

а) могут пересекаться под произвольным углом φ;

б) под прямым углом, т.е. взаимно перпендикулярны.

а) За угол между прямой и плоскостью принимается угол α между этой прямой и её проекцией на плоскость.

При этом за угол берут наименьший из углов, которые прямая образует с плоскостью, т.е. . Угол между нормальным вектором плоскости и направляющим вектором прямой обозначим через φ. Тогда - дополнительные углы. Из формул тригонометрии имеем: . При этом . - формула вычисления угла между прямой и плоскостью.

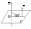
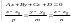б) Если прямая перпендикулярна плоскости, то её направляющий вектор коллинеарен направляющему вектору плоскости Р, т.е. . Из условия коллинеарности следует : . Для того чтобы найти точку М пересечение прямой с плоскостью нужно решить совместно уравнения прямой и плоскости:

Для этого записать уравнение прямой в параметрической форме и подставить значения x,y,z в первое уравнение.

Решая это уравнение относительно t и подставляя найденное t в систему, получим - координаты точки пересечения М.

3. Они могут иметь бесчисленное множество точек, т.е. прямая лежит в плоскости.

10.

Окружностью называется геометрическое место точек, расстояние которых до фиксированной точки, называемой центром, есть величина постоянная, равная R.

- каноническое уравнение окружности.

Где a и b – координаты центра, а R – радиус.

Особенности:

1.Оно обязательно содержит квадраты переменных и с одинаковыми знаками и коэффициентами.

2.Оно не содержит члена с произведением координат ху.

11.Эллипсом называется геометрическое место точек, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная(она должна быть больше расстояния между фокусами) .

- каноническое уравнение эллипса.

Вывод: ,

обе части возводим в квадрат

раскрываем скобки и сокращаем

делим на 4 и обе части возводим в квадрат

раскрываем скобки и сокращаем

замена

делим на и получаем

где а и b – это полуоси эллипса, причем а на оси OX, а b на оси OY.

Большая ось эллипса является фокальной, т.е. на этой оси расположены его фокусы, и он всегда вытянут вдоль фокальной оси. Параметры эллипса a,b,c связаны между собой. Зная два из них , можно всегда найти третий. В зависимости от фокальной оси формулы связывающие параметры меняются. Если фокусы эллипса лежат на оси OX, то выполняется равенство . Если фокусы на оси OY,то . Особенности: оно всегда содержит сумму квадратов переменных и , коэффициенты при которых различные, в отличии от уравнения окружности. Если центр эллипса находится не в начале координат, то его уравнение имеет вид: .

Эксцентриситетом эллипса называется отношение межфокусного расстояния к длине большей оси.

если фокусы на OX

если фокусы на OY

Эксцентриситет эллипса всегда положителен, но меньше 1, т.к. c<a(c<b), т.е. 0< <1. Он характеризует форму эллипса. Чем больше эксцентриситет, тем больше вытянут эллипс вдоль фокальной оси. Если , если =1, то эллипс вырождается в прямую линию. Если a=b, то эллипс превращается в окружность.

12.

Гиперболой называется геометрическое место точек, разность расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (она должна быть положительной и меньше расстояния между фокусами) .

каноническое уравнение гиперболы.

Вывод гиперболы выводится аналогично эллипсу.

Ось, на которой расположены фокусы, называется действительной, другая ось – мнимой.

Если фокусы расположены на оси OY, то уравнение принимает вид: .

Связь между параметрами у гиперболы постоянная, т.е. не зависит от фокальной оси. Межфокусное расстояние является самым большим параметром .

Эксцентриситетом гиперболы называется отношение межфокусного расстояния к длине действительной оси.

если фокусы на OX

если фокусы на OY

Эксцентриситет гиперболы всегда положителен и больше 1, т.к. с>a и c>b, т.е. >1.

13.

Прямая называется асимптотой, если при удалении точки в бесконечность расстояние между точками кривой и прямой становится бесконечно малым, т.е. стремится к 0.

Большую роль у гиперболы играют асимптоты, т.к. они направляют ветви гиперболы. Уравнение асимптот не зависят от фокальной оси и имеют вид . Построение гиперболы начинают с асимптот. Если построить прямоугольник со сторонами, параллельными координатным осям и равными 2a и 2b, то его диагонали будут асимптотами гиперболы. Если гипербола смещена в системе координат, то её каноническое уравнение имеет вид , где - координаты центра гиперболы.

14.

Параболой называется геометрическое место точек, равноотстоящих от данной точки, называемой фокусом и от данной прямой, называемой директрисой.

- каноническое уравнение параболы.

- уравнение директрисы.

Вывод: MF=MK

;

раскрываем скобки и сокращаем

.

Эксцентриситет параболы всегда равен 1. Для составления уравнения параболы нужно знать её параметр и фокальную ось.