
- •Первый закон термодинамики. Внутренняя энергия-функция состояния системы.
- •Энтальпия.
- •4. Приложение первого закона термодинамики к идеальным газам (изохорный, изобарный процессы).
- •5. Приложение первого закона термодинамики к идеальным газам (изотермический, адиабатический процессы).
- •6. Теплоемкость и ее зависимость от температуры.
- •7. Закон Гесса – основной закон термохимии.
- •8.Уравнение Кирхгоффа в дифференциальной форме.
- •9.Уравнение Киргоффа в интегральной форме.
- •10.Второй з-н термодинамики. Понятие и определение.
- •11. Работа обратимого и необратимого процесса.
- •12. Цикл Карно.
- •13. Энтропия обратимых процессов.
- •14. Энтропия необратимых процессов.
- •15. Смысл энтропии:
- •16.Вычисление энтропий в различных условиях.
- •17. Свободная энергия Гельмгольца.
- •18. Свободная энергия Гиббса.
- •19. Уравнения Гиббса- Гельмгольца.
- •20. Химический потенциал.
- •21. Химический потенциал идеального и реального газа. Летучесть(или фугетивность).
- •22. Закон действующих масс. Константа равновесия.
- •23. Изотерма химической реакции Вант-Гофа.
- •24. Уравнение изобары.
- •25. Уравнение изохоры.
- •1Первый закон термодинамики. Внутренняя энергия-функция состояния системы.
18. Свободная энергия Гиббса.
Близко к изохорному потенциалу является функция, которая определяет направление и предел самопроизвольного протекания процессов для систем, находящихся при
Р, Т = const.
dU=TdS-PdV;
dU-TdS+PdV=0;
d(U-TS+PV)=0;
Т.е существует такая функция состояния, полный дифференциал которой равен 0.
G= U-TS+PV -свободной энергии Гиббса.
G=F+PV;
Свободная энергия Гиббса так же, как энергия Гельмгольца, является полным дифференциалом.
dG=dF+PdV;
![]()
Av=-![]() F;
F;
Ap=![]()
АР –max полезная работа, совершающаяся в изотермических условиях.
Ap=Av-P V (6);
Max полезная работа = max работе ( при V, T= const) за вычетом работы против внешнего давления. В закрытых системах, находящихся при V, T= const, самопроизвольно могут протекать процессы, сопровождающиеся уменьшением свободной энергии Гиббса. Пределом их протекания является достижение некоторого минимального значения.
G<0 процесс протекает самопроизвольно необратимо.
G=0 для обратимых процессов в момент наступления химического равновесия.
G=U-TS+PV;
G=H-TS;
dG=dH-TdS;
![]()
G=f(P,T);
dG=![]() (7);
(7);
dG=TdS-PdVTdS-SdT+PdV+VdP;
dG=-SdT+VdP (8);
Решим совместно уравнения (7) и ( 8 ).
(![]() )p=-S;
(
)p=-S;
(![]() )T=V;
(9)
)T=V;
(9)
Из формулы (9) следует, что энтропия является мерой убыли свободной энергии Гиббса при изобарных условиях, а объем мерой ее возрастания при повышении давления в изотермических условиях.
19. Уравнения Гиббса- Гельмгольца.
Данное уравнение выражает зависимость термодинамических потенциалов от температуры в дифференциальной форме.
F=U-TS=U+T( )v;
![]() (
(![]() )v=Qv+T(
)v=
Qv-T(
)v=Qv+T(
)v=
Qv-T(![]() )v;
)v;
U=Qv;
Av=- F;
Уравнения Гиббса- Гельмгольца имеет значение в изотермических процессах, где их протекание сопровождается совершением работы при видимом отсутствии в изменении объема ( работа совершающаяся в гальваническом элементе).
G=H-TS;
G=H+T( )p;
G=Qp+T(![]() )p;
)p;
Ap=- G;
Уравнение Гиббса- Гельмгольца позволяет устанавливать взаимосвязь между термодинамическим потенциалом max работы процессов, протекающих равновесно и теплотой того же процесса, протекающей не равновесно.
20. Химический потенциал.
1,2 законы термодинамики
справедливы только для изолированных
и закрытых систем. 1-ый закон термодинамики
устанавливает существование функции
состояния внутренней энергии, 2-ой –
энтропии. Вероятно, что данные функции
будут существовать и открытых системах,
где кроме энергообмена сущ. и массообмен
(изменяется число моль в в-ве). Рассмотрим
открытую систему, процессы в которой
совершаются при постоянном давлении и
Т. G=(p,T,n1,n2,ni).
![]() -число
моль компонентов образующих систему.
-число
моль компонентов образующих систему.
dG=(δG/δp)T,nidp+
(δG/δT)p,n
dt
+![]() nj=n1-1
nj=n1-1
![]() -величина
химического потенциала. Величина
химического потенциала – частная
производная изобарно изотермического
потенциала по числу молей компонентов
при постоянстве давления , температуры
и всех компонентов за исключением
одного.
-величина
химического потенциала. Величина
химического потенциала – частная
производная изобарно изотермического
потенциала по числу молей компонентов
при постоянстве давления , температуры
и всех компонентов за исключением
одного.
Если Р,Т=const
![]() Т. к. энергия Гиббса явл. критерием
протекания или направленности протекания
процессов (∆G<=0)
значит в момент равновесия
Т. к. энергия Гиббса явл. критерием
протекания или направленности протекания
процессов (∆G<=0)
значит в момент равновесия
![]() .
Для самопроизвольных процессов это
выр-ние <0. Для выяснения физического
смысла химического потенциала
проинтегрируем выр-ние dGi=μidni
.
Для самопроизвольных процессов это
выр-ние <0. Для выяснения физического
смысла химического потенциала
проинтегрируем выр-ние dGi=μidni
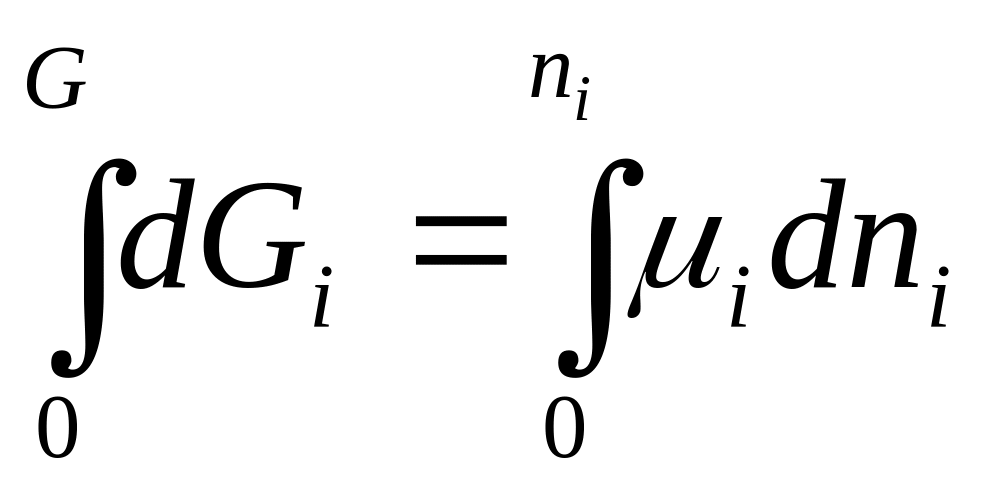 Gi=μini.
Если ni=1
значит Gi=μi.
Химический потенциал равен
изобарно-изотермическому потенциалу
если число компонентов =1. В открытых
системах критерием направленности и
возможности протекания процессов явл.
химический потенциал, при постоянном
Р и Т (V
и T).
Gi=μini.
Если ni=1
значит Gi=μi.
Химический потенциал равен
изобарно-изотермическому потенциалу
если число компонентов =1. В открытых
системах критерием направленности и
возможности протекания процессов явл.
химический потенциал, при постоянном
Р и Т (V
и T).
