Возрастание и убывание функции

Для того, чтобы дифференцируемая на интервале (a; b) функция f была неубывающей на этом интервале, необходимо и достаточно, чтобы выполнялось условие

для любого

Аналогичным образом определяется необходимое и достаточное условие невозрастания функции f:

Экстремумы

Напомним, что в точке x₀ функция достигает экстремума, если для любых x из некоторой окрестности точки x₀ выполняется неравенство f (x) ≤ f (x₀) (минимум) или f (x) ≥ f (x₀) (максимум).

Теорема Ферма. Если функция f (x) дифференцируема в точке x₀ и достигает в ней экстремума, то

Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю.

Обратное, вообще говоря, неверно. Так, точка x = 0 функции y = x³ не является ни максимумом, ни минимумом.

Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Таким образом, все экстремумы являются критическими точками

Достаточные условия экстремума. Пусть функция дифференцируема в некоторой окрестности точки x₀, кроме, быть может, самой этой точки, и непрерывна в точке x₀. Если производная функции меняет знак с минуса на плюс при переходе через эту точку слева направо, то x₀ – точка минимума. Если производная функции меняет знак с плюса на минус при переходе через эту точку слева направо, то x₀ – точка максимума.

Утверждение. Пусть – стационарная точка функции f (x), и существует Если то – точка минимума; если то – точка максимума функции f (x).

Выпуклость функции и точки перегиба

Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x₁ и x₂ из этого отрезка

Другими словами, если для любых точек x₁ и x₂ отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла .

Аналогично определяется функция вогнутая.

Определение. Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого

Определение. Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого

Так, вторая производная функции равна откуда следует, что квадратичная функция выпукла вниз на всей области определения.

Определение. Пусть функция f (x) непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда точка называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.

Необходимое условие наличия точки перегиба. Если – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то

Достаточные условия наличия точки перегиба.

Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке  Если меняет знак при переходе через точку  то – точка перегиба функции f (x).

При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:

1. Найти область определения функции.

2. Определить четность или нечетность функции.

3. Найти точки пересечения графика с осями координат, если это возможно.

4. Исследовать функцию на непрерывность. Найти асимптоты графика функции.

5. Найти интервалы монотонности и точки экстремума функции.

6. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

7. Найти значение функции в нескольких дополнительных точках.

На основании полученного исследования построить график.

Пример 1. Исследовать функцию и построить ее график:

.

Решение.

1. Найдем область определения функции. Это будет вся числовая ось, кроме точек, в которых знаменатель обращается в 0.

. .

2. Функция является нечетной, т.к. , ее график симметричен относительно начала координат (значит, график можно построить только при х≥0, а затем в силу нечетности функции отобразить его симметрично относительно начала координат).

3. Точка пересечения с осями координат: - начало координат.

4. Асимптоты графика:

а) вертикальные

б) наклонные , где

.

-горизонтальная асимптота - ось - при .

5. Проведем полное исследование по первой производной.

Нетрудно заметить, что при любом значении области определения функции, производная , т.е. функция является всюду возрастающей. Точек экстремума нет.

8. Проведем полное исследование по второй производной.

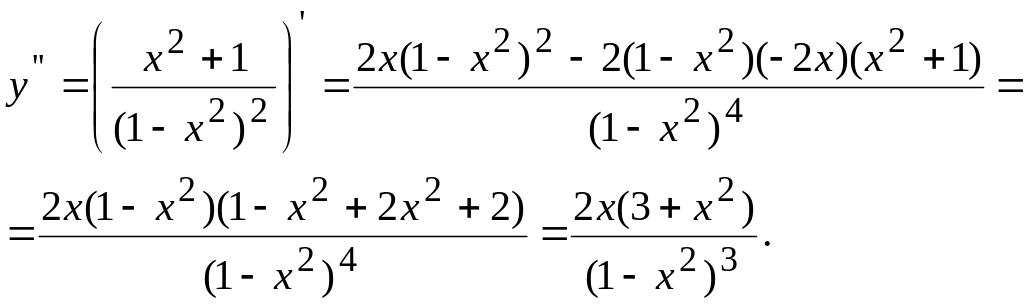
при .

Выделим интервалы:

Точка является точкой перегиба графика функции . Нанесем на чертеж все полученные точки и линии