13 Общее уравнение прямой:
Ах + Ву + С = 0 ,
где А и В не равны нулю одновременно.
Коэффициенты А и В являются координатами нормального вектора прямой ( т.е. вектора, перпендикулярного прямой ). При А = 0 прямая параллельна оси ОХ , при В = 0 прямая параллельна оси ОY .
При
В
0
получаем
уравнение
прямой с угловым коэффициентом:
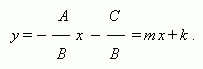
Уравнение прямой, проходящей через точку ( х0 , у 0 ) и не параллельной оси OY, имеет вид:
у – у 0 = m ( x – х0 ) ,
где m – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .
При А 0, В 0 и С 0 получаем уравнение прямой в отрезках на осях:
где a = – C / A , b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной a и b .
Уравнение прямой, проходящей через две различные точки ( х1, у 1 ) и ( х2, у 2 ):
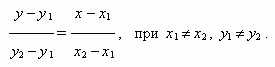
Параметрическое уравнение прямой, проходящей через точку ( х0 , у 0 ) и параллельной направляющему вектору прямой ( a, b ) :
Условие параллельности прямых:
1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0 : AE – BD = 0 ,
2) для прямых у = m x+ k и у = p x+ q : m = p .
Условие перпендикулярности прямых:
1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0 : AD + BE = 0 ,
2) для прямых у = m x+ k и у = p x+ q : m p = – 1 .
Расстояние между двумя точками ( x1, y 1 ) и ( x2 , y2 ) :
Расстояние от точки ( х0 , у 0 ) до прямой Ах+ Ву+ С = 0 :
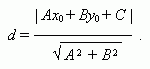
Расстояние между параллельными прямыми Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0 :
Угол
между
прямыми:
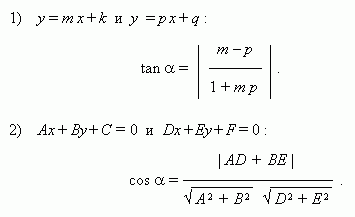
26 Первый замечательный предел
Доказательство
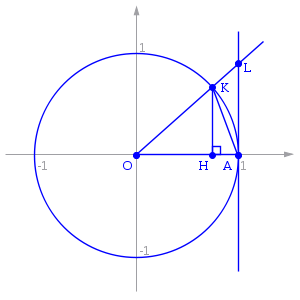
Рассмотрим
односторонние
пределы
и
и
докажем, что они равны 1.
Пусть
.
Отложим этот угол на единичной окружности
(R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
(1)
(где SsectOKA — площадь сектора OKA)
(из
:
| LA | = tgx)
Подставляя в (1), получим:
Так
как при
:
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
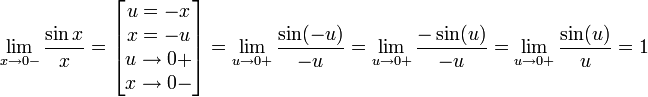
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
27 Второй замечательный предел
или
Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
Докажем
вначале теорему для случая последовательности
По
формуле бинома
Ньютона:
Полагая
,
получим:
(1)
Из
данного равенства (1) следует, что с
увеличением n число положительных
слагаемых в правой части увеличивается.
Кроме того, при увеличении n число
убывает,
поэтому величины
возрастают.
Поэтому последовательность
—
возрастающая,
при этом
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
.
Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:
.
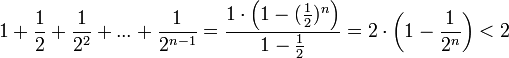Поэтому
(3).
Итак,
последовательность ограничена сверху,
при этом
выполняются
неравенства (2) и (3):
.
Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
.
Рассмотрим два случая:
1.
Пусть
.
Каждое значение x заключено между двумя
положительными целыми числами:
,
где
—
это целая часть x.
Отсюда
следует:
,
поэтому
.
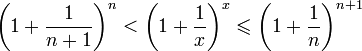Если
,
то
.
Поэтому, согласно пределу
,
имеем:
.
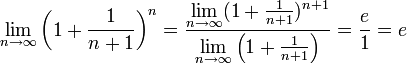
По
признаку (о пределе промежуточной
функции) существования пределов
.
2.
Пусть
.
Сделаем подстановку − x = t, тогда
.
Из двух этих случаев вытекает, что для вещественного x.
Следствия
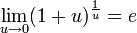
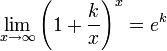
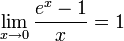
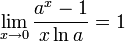для
,
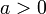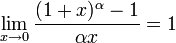
28
Непрерывность функций |
||||||
|
||||||
Определение непрерывности по Гейне Говорят,
что функция действительного переменного
f
(x)
является непрерывной
в точке
выполняется соотношение
На практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a :
Определение
непрерывности по Коши (нотация
Рассмотрим
функцию f
(x),
которая отображает множество
действительных чисел
на
другое подмножество B
действительных чисел. Говорят, что
функция f
(x)
является непрерывной
в точке
,
если для любого числа
выполняется неравенство
Определение непрерывности в терминах приращений аргумента и функции Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке x = a, если справедливо равенство
где
Теоремы непрерывности Теорема
1.
Пусть функция f
(x)
непрерывна в точке x
= a,
и C
является константой. Тогда функция
Сf
(x)
также непрерывна при x
= a.
Теорема
2.
Даны две функции f
(x)
и g
(x),
непрерывные в точке x
= a.
Тогда сумма этих функций f
(x)
+ g
(x)
также непрерывна в точке x
= a.
Теорема
3.
Предположим, что две функции f
(x)
и g
(x)
непрерывны в точке x
= a.
Тогда произведение этих функций f
(x)
g
(x)
также непрерывно в точке x
= a.
Теорема
4.
Даны две функции f
(x)
и g
(x),
непрерывные при x
= a.
Тогда отношение этих функций
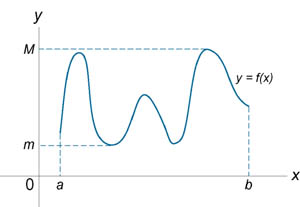
для всех x в интервале [a, b] (смотрите рисунок 1).
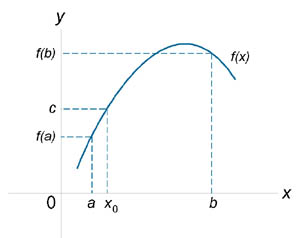
Теорема 7 (Теорема о промежуточном значении). Пусть функция f (x) непрерывна на закрытом и ограниченном интервале [a, b]. Тогда, если c − некоторое число, большее f (a) и меньшее f (b), то существует число x0, такое, что
Данная теорема проиллюстрирована на рисунке 2. Непрерывность элементарных функций Все элементарные функции являются непрерывными в любой точке свой области определения. Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:
30 |
(
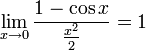
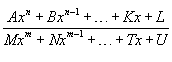- множество действительных чисел),
если для любой последовательности
,
такой, что
существует;
.
)
существует
число
,
такое, что для всех
,
удовлетворяющих соотношению
.
Приведенные определения
непрерывности функции эквивалентны
на множестве действительных чисел.
Функция является непрерывной
на данном интервале,
если она непрерывна в каждой точке
этого интервала.
также
непрерывно при x
= a
при условии, что
.
Теорема
5.
Предположим, что функция f
(x)
является дифференцируемой в точке x
= a.
Тогда функция f
(x)
непрерывна в этой точке (т.е. из
дифференцируемости следует непрерывность
функции в точке; обратное − неверно).
Теорема
6 (Теорема о предельном значении).
Если функция f
(x)
непрерывна на закрытом и ограниченном
интервале [a,
b],
то она ограничена сверху и снизу на
данном интервале. Другими словами,
существуют числа m
и M,
такие, что
;
;
;
;
;
;
;
;
.