11 Нормальное уравнение прямой. Расстояние от точки до прямой
Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.
Если
![]() -
полярный угол нормали, р - длина отрезка
-
полярный угол нормали, р - длина отрезка
![]() (рис.),
то уравнение данной прямой может быть
записано в виде
(рис.),
то уравнение данной прямой может быть
записано в виде
![]() ;
;
уравнение этого вида называется нормальным.
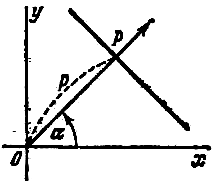
Пусть
дана какая-нибудь прямая и произвольная
точка
![]() ;
обозначим через d
расстояние от точки М* до данной прямой.
Отклонением
;
обозначим через d
расстояние от точки М* до данной прямой.
Отклонением
![]() точки
от
прямой называется число +d,
если данная точка и начало координат
лежат по разные стороны от данной прямой,
и -d,
если данная точка и начало координат
расположены по одну сторону от данной
прямой. (Для точек, лежащих на самой
прямой,
=0).
Если даны координаты
точки
от
прямой называется число +d,
если данная точка и начало координат
лежат по разные стороны от данной прямой,
и -d,
если данная точка и начало координат
расположены по одну сторону от данной
прямой. (Для точек, лежащих на самой
прямой,
=0).
Если даны координаты
![]() ,
,
![]() точки
и
нормальное уравнение прямой
,
то отклонение
точки
от
этой прямой может быть вычислено по
формуле
точки
и
нормальное уравнение прямой
,
то отклонение
точки
от
этой прямой может быть вычислено по
формуле
![]() .
.
Таким образом, чтобы найти отклонение какой-нибудь точки от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки . Полученное число будет равно искомому отклонению.
Чтобы
найти расстояние d
от точки до прямой, достаточно вычислить
отклонение и взять его модуль:
![]() .
.
Если
дано общее уравнение прямой
![]() ,
то, чтобы привести его к нормальному
виду, нужно все члены этого уравнения
умножить на нормирующий множитель
,
то, чтобы привести его к нормальному
виду, нужно все члены этого уравнения
умножить на нормирующий множитель
![]() ,
определяемый формулой
,
определяемый формулой
![]() .
.
Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.
12 Вычисление угла между прямыми
Пусть
прямые
![]() и
и
![]() заданы
общими уравнениями
заданы
общими уравнениями
|
Обозначим
через φ величину угла между прямыми
и
(напомним,
что угол между прямыми измеряется от
0° до 90°), а через ψ – угол между нормальными
векторами
![]() и
и
![]() этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство
этих
прямых. Если ψ ≤ 90°, то φ = ψ.
Если же ψ > 90°, то φ = 180° – ψ.
В обоих случаях верно равенство
![]() Из
теоремы
11.10 следует, что
Из
теоремы
11.10 следует, что
|
и, следовательно,
|
Записав через координаты, получим
|
Если
прямые
и
заданы
уравнениями с угловыми коэффициентами
![]() и
и
![]()
|
то
нормальные векторы этих прямых могут
быть
![]()
![]() и
выражение для косинуса угла между этими
прямыми будет иметь вид:
и
выражение для косинуса угла между этими
прямыми будет иметь вид:
|
Из
последнего выражения следует, что если
![]() то
cos φ = 1 и φ = 0, то есть прямые
параллельны или совпадают. С другой
стороны, если прямые параллельны, то
φ = 0 или cos φ = 1. Подставляя
в правую часть вместо cos φ его значение
1, умножая обе части на знаменатель и
возводя в квадрат, получим
то
cos φ = 1 и φ = 0, то есть прямые
параллельны или совпадают. С другой
стороны, если прямые параллельны, то
φ = 0 или cos φ = 1. Подставляя
в правую часть вместо cos φ его значение
1, умножая обе части на знаменатель и
возводя в квадрат, получим
|
Отсюда
получаем
![]()
Если
![]() то
cos φ = 0 и
то
cos φ = 0 и
![]() то
есть прямые перпендикулярны. Обратно,
если прямые перпендикулярны, то
то
есть прямые перпендикулярны. Обратно,
если прямые перпендикулярны, то
![]() или
cos φ = 0. Отсюда следует с
необходимостью
или
cos φ = 0. Отсюда следует с
необходимостью
![]()
Следовательно,
необходимые и достаточные условия
параллельности и перпендикулярности
двух прямых, заданных уравнениями с
угловыми коэффициентами
и
![]() формулируются
следующим образом.
формулируются
следующим образом.
Т![]() еорема 11.13.
еорема 11.13.
Для
того чтобы прямые
![]() и
и
![]() были
были
параллельны, необходимо и достаточно, чтобы
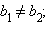
перпендикулярны, необходимо и достаточно, чтобы

Пользуясь знанием координат направляющего и нормального векторов прямых, заданных общими уравнениями, можно сформулировать условия параллельности и перпендикулярности прямых через коэффициенты общих уравнений этих прямых.
Т еорема 11.14.
Для
того чтобы прямые
![]() и
и
![]() были
были
параллельны, необходимо и достаточно, чтобы соответствующие коэффициенты их уравнений при одноименных неизвестных были пропорциональны, то есть

перпендикулярны, необходимо и достаточно, чтобы выполнялось равенство
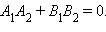
Доказательство
|
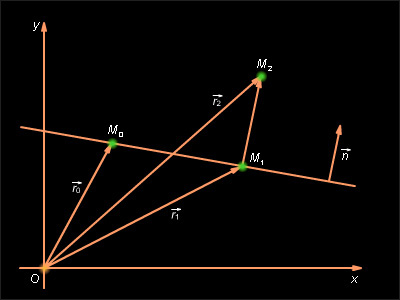
Пусть
задана прямая l
общим уравнением Ax + By + C = 0
и некоторая точка
![]() лежащая
вне прямой. Поставим задачу найти
расстояние
лежащая
вне прямой. Поставим задачу найти
расстояние
![]() от
этой точки до прямой l.
Опустим перпендикуляр
от
этой точки до прямой l.
Опустим перпендикуляр
![]() из
точки
из
точки
![]() на
прямую l
и обозначим
на
прямую l
и обозначим
![]()
![]() радиус-векторы
точек
радиус-векторы
точек
![]() и
соответственно
(см. рис. 11.6.1). Очевидно,
и
соответственно
(см. рис. 11.6.1). Очевидно,
![]()
1 |
Рисунок 11.6.1. |
Пусть
![]() –
некоторая точка прямой l,
отличная от точки
–
некоторая точка прямой l,
отличная от точки
![]() Тогда
уравнение прямой l
можно записать в нормальной векторной
форме:
Тогда
уравнение прямой l
можно записать в нормальной векторной
форме:
|
где
![]() а
а
![]() –
вектор нормали к прямой l.
Или, в векторной форме,
–
вектор нормали к прямой l.
Или, в векторной форме,
![]()
Очевидно,
справедливо векторное равенство
![]() причем
причем
![]() поэтому
поэтому
![]() Умножив
обе части равенства скалярно на вектор
Умножив
обе части равенства скалярно на вектор
![]() , получим
, получим
|
Так
как точка
лежит
на прямой l,
то
![]() и,
следовательно,
и,
следовательно,
![]() Подставляя
в исходное равенство, найдем
Подставляя
в исходное равенство, найдем
|
Отсюда
|
Переходя
к координатной форме записи и учитывая,
что
![]() имеем
имеем
|
Таким образом верна теорема
Т еорема 11.15.
Растояние
от
точки
![]() до
прямой l,
заданной уравнением Ax + By + C = 0
вычисляется по формуле
до
прямой l,
заданной уравнением Ax + By + C = 0
вычисляется по формуле
|


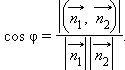

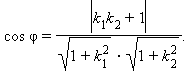

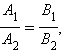

 то
прямые параллельны.
то
прямые параллельны.