Емкость p-n-перехода.

Диод обладает емкостными свойствами, т.е. способен накапливать и отдавать заряд при увеличении или уменьшении приложенного напряжения. Накопление заряда происходит в p-n-переходе и в базе диода, и в соответствие с этим различают две составляющие емкости – барьерную и диффузионную:

C_Д=C_бар+C_дф

Барьерная емкость. При изменении напряжения меняется толщина (ширина) p-n-перехода и в соответствие с этим меняется некомпенсированный заряд ионов донорных и акцепторных примесей в переходе. Дифференциальную емкость C_бар можно рассматривать как емкость плоского конденсатора с обкладками, расположенными на расстоянии, равном толщине перехода :

C_бар=₀S/, (2.33)

где  – диэлектрическая проницаемость, ₀ – диэлектрическая постоянная, S – площадь перехода.

Подставляя  для резкого одностороннего перехода, получаем

, (2.34)

где N – концентрация легирующей примеси в базе, C₀ – емкость при U=0.

В общем случае

, (2.35)

где =1/2 для резкого перехода и =1/3 – для плавного.

Диффузионная емкость обусловлена накоплением неравновесных носителей в базе. Объем при этом сохраняет электронейтральность – заряд накапливается не в виде электрического заряда, а в виде избыточной концентрации носителей.

Для статического режима нетрудно найти заряд, накопленный в базе, проинтегрировав функцию распределения неравновесных носителей (2.17) по x

.

Выразив затем p(0) через ток I=eSj_p(0)=eSD_pp(0)/L_p, получаем

, (2.36)

где =L_p²/D_p – время жизни неравновесных носителей в базе (индекс p для общности опущен).

Эта формула относится к диодам с толстой базой, когда толщина базы (расстояние до омического контакта) w>>L, где L – диффузионная длина неравновесных носителей. Дифференцируя (2.36) по U получаем

C_дф=(I+I₀)/_T (2.37)

При обратном соотношении w<<L распределение концентрации в базе является практически линейным, и Q_б=I_дф, где _дф – среднее время диффузии через базу:

_дф=w²/(2D) (2.38)

В этом случае

C_дф=(I+I₀)_дф/_T (2.39)

C_дф и C_бар проявляются в разных режимах работы: C_дф>> C_бар при I>>I₀, и C_бар>> C_дф при U<0. C_дф нельзя считать «чистой» емкостью, так как она зависит от частоты или длительности импульса в импульсном режиме работы.

2.2. Контакты металл-полупроводник

Контакты металл-полупроводник могут быть выпрямляющими, которые называются также контактами Шоттки, и невыпрямляющими, или омическими. Тип контакта зависит от разности термоэлектронных работ выхода электрона из металла A_M и из полупроводника A_S и от типа проводимости полупроводника. Термоэлектронная работа выхода – это разность между энергией электрона в вакууме и уровнем Ферми:

A=W_вак-W_F (2.40)

Чем больше A, тем меньше энергия электронов, поэтому электроны переходят в область с большей работой выхода: если A_M>A_S, электроны переходят из полупроводника в металл, если A_M<A_S, – из металла в полупроводник. В равновесии уровни Ферми выравниваются, между областями возникает контактная разность потенциалов:

_к= (A_MA_S) e (2.41)

Слой полупроводника, прилегающий к контакту, обогащается или обедняется основными носителями и образуется омический или выпрямляющий контакт. Если A_M>A_S, то контакт M-n – выпрямляющий, M-p – омический. Если A_M<A_S, контакт M-n – омический, M-p – выпрямляющий.

Н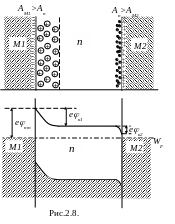 а рис.2.8 показаны оба типа контакта с полупроводником n-типа (эта структура представляет собой диод Шоттки) и приведена энергетическая диаграмма.

В выпрямляющем контакте обедненный слой расположен целиком в полупроводнике. Он обладает высоким сопротивлением и нелинейной ВАХ. Толщина этого слоя определяется так же, как толщина p-n-перехода:

, (2.42)

где N – концентрация легирующей примеси в полупроводнике.

Потенциальный барьеры для электронов, движущихся из металла в полупроводник и из полупроводника в металл различны и равны, соответственно, _nm и _к1. Высота барьера _nm определяется выражением

_nm = (A_M_n )/e, (2.43)

где _n. называется энергией электронного сродства, или сродством к электрону, и определяется как минимальная энергия, необходимая для удаления электрона со дна зоны проводимости полупроводника в вакуум. При приложении внешнего напряжения изменяется потенциальный барьер для электронов, движущихся из полупроводника в металл, а для обратного направления остается неизменным, поскольку все приложенное напряжение падает в обедненном слое полупроводника. На рис.2.9 приведены энергетические диаграммы выпрямляющего контакта при подаче прямого (плюс источника подан на металл, U>0) (а) и обратного (U<0) напряжения (б). При обратном включении ток обусловлен электронами, имеющими энергию выше потенциального барьера e_nm.

Теория выпрямляющего контакта базируется на теории термоэлектронной эмиссии электронов. Вольтамперная характеристика описывается такой же функцией, как ВАХ идеализированного p-n-перехода, причем эта зависимость выполняется с большой точностью в широком интервале токов (до восьми порядков величины тока):

(2.44)

Ток I₀ определяется током термоэлектронной эмиссии из металла в полупроводник:

, (2.45)

где A_R – постоянная Ричардсона, для кремния n-типа A_R=110 А/(см² ·К), S – площадь контакта.

При равной площади, температуре и степени легирования полупроводника обратный ток контакта Шоттки значительно больше теплового тока кремниевого p-n-перехода. Поэтому напряжение отпирания контакта Шоттки с кремнием ниже, чем кремниевого p-n-перехода.

Омический контакт имеет линейную ВАХ и малое сопротивление. Особенностью этого контакта является также высокая скорость генерации и рекомбинации, поэтому концентрация носителей на границе сохраняется практически неизменной и при протекании тока.

Следует особо отметить, что контакты металл-полупроводник работают на основных носителях заряда, через эти контакты нет инжекции неосновных носителей, нет накопления неравновесного заряда в полупроводнике. Контакт Шоттки обладает только барьерной емкостью. Поэтому диоды Шоттки обладают высоким быстродействием.