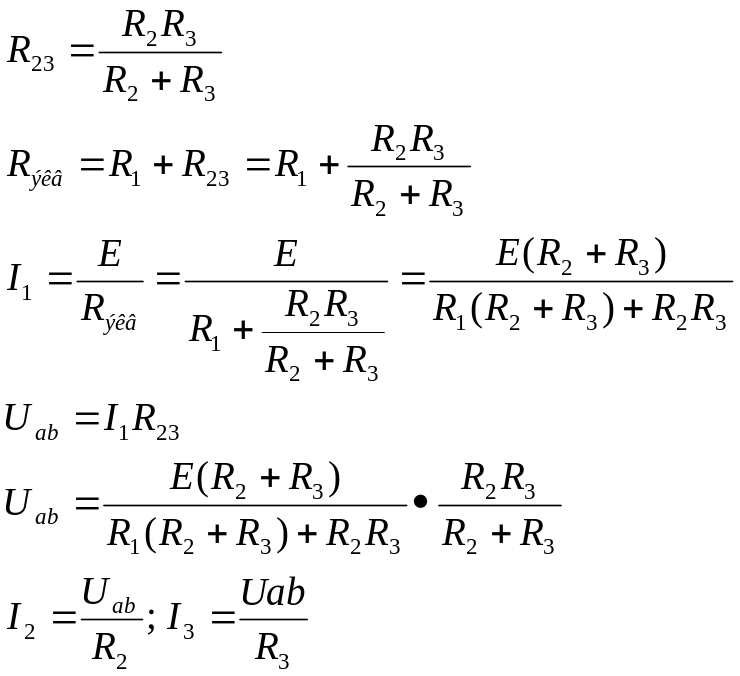Применение законов Кирхгофа для анализа цепей постоянного тока.

Для цепи постоянного тока можно записать законы Кирхгофа:

1. Алгебраическая сумма токов, сходящихся в узле, равна 0. - число ветвей, сходящихся в узле.

2.

Алгебраическая сумма напряжения на пассивных участках контура равна алгебраической сумме ЭДС, действующих в электрическом контуре.

Порядок расчета:

Пусть электрическая цепь постоянного тока содержит x ветвей. Для ее расчета по законам Кирхгофа необходимо составить x линейно независимых уравнений по законам Кирхгофа.

1. Выбираем «+» направление токов в ветвях, записываем N-1-е уравнение по первому закону Кирхгофа, где N – число узлов в цепи.

2. Остальные уравнения запишем по второму закону Кирхгофа. Их число C=x-(N-1) и равно числу неизвестных контуров цепи.

3. Решаем систему алгебраических уравнений, находим токи во всех ветвях. Если какой- либо ток в результате расчета оказался «-», то его действительное значение противоположно выбранному за условно «+».

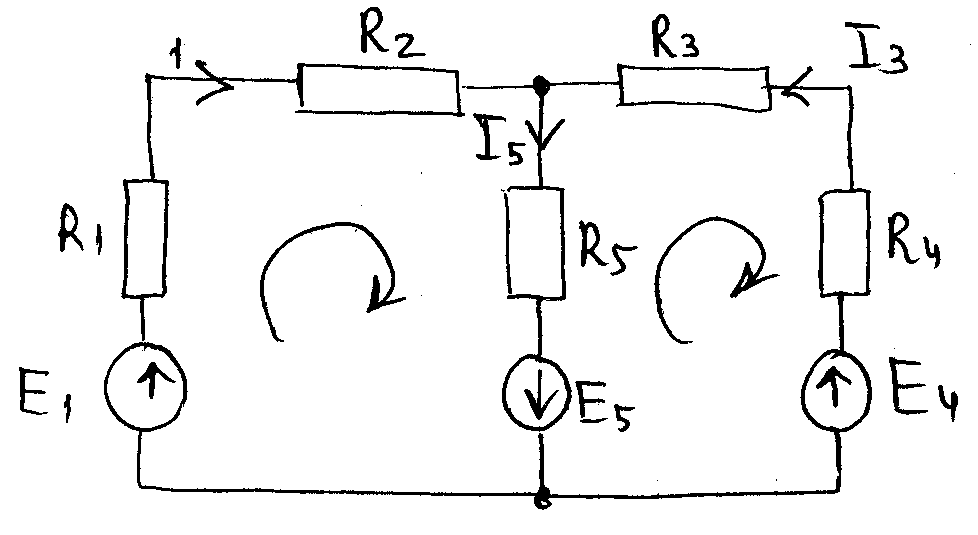
Электрическая цепь содержит 3 ветви, должны составить 3 линейных, но независимых уравнений. 2 узла.

I₁+I₃-I₅=0

(R₁+R₂)I₁+R₅I₅=E₁+E₅

-R₅I₅-(R₃+R₄)I₃=-E₄-E₅

Метод контурных токов.

Метод контурных токов следует из законов Кирхгофа и принципа наложения. Этот метод позволяет сократить число решаемых уравнений. Уравнения составляются относительно контурных токов. Число уравнений равно числу уравнений, которые необходимо было бы составить по 2 закону Кирхгофа. Предполагается, что в каждом независимом контуре протекает свой контурный ток, составляется система уравнений относительно контурных токов. После написания контурных токов рассчитываются токи в ветвях.

Для получения основных расчетных соотношений рассмотрим схему:

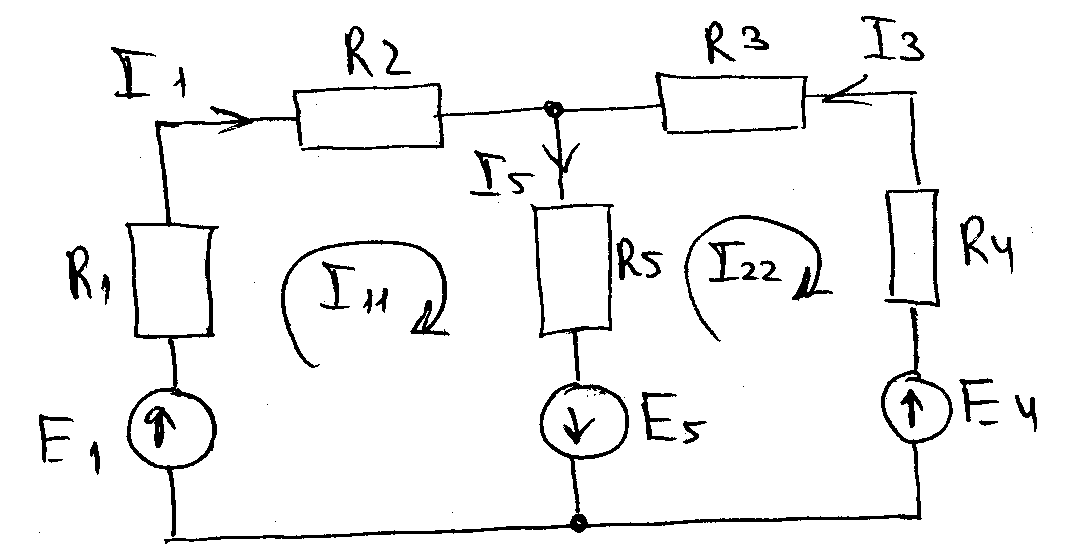
Схема содержит 2 независимых контура.

Предполагается, что в каждом протекает свой контурный ток I₁₁ и I₂₂.

Токи в ветвях могут быть выражены через контурные токи следующим образом:

I₁=I₁₁; I₃=-I₂₂; I₅=I₁₁-I₂₂.

В несмежных ветвях токи в ветвях равны противоположным по знаку контурным токам. В смежной ветви ток ветви равен разности контурных токов.

Обозначим:

<обрезалось> 1-го контура.

<обрезалось> = сумме сопротивлений всех ветвей.

R₂₂=R₃+R₄+R₅ – полное (контурное) сопротивление 2-го контура = сумме сопротивлений всех ветвей контура.

R₁₂=R₂₁=-R₅ – сопротивление смежной ветви со знаком «-».

E₁₁=E₁+E₅ – контурная ЭДС – алгебраическая сумма ЭДС контура.

E22=-E4-E5 – контурная ЭДС 2-го контура.

В общем случае, если электрическая цепь содержит N независимых контуров, составляется система уравнений для N контурных токов.

Правило: составляется сумма произведений контурных токов на сопротивления и сопротивления смежных ветвей с соответствующими знаками, и эта сумма приравнивается контурной ЭДС. В результате решения системы уравнений находятся контурные токи. Токи в ветвях выражаются через контурные токи.

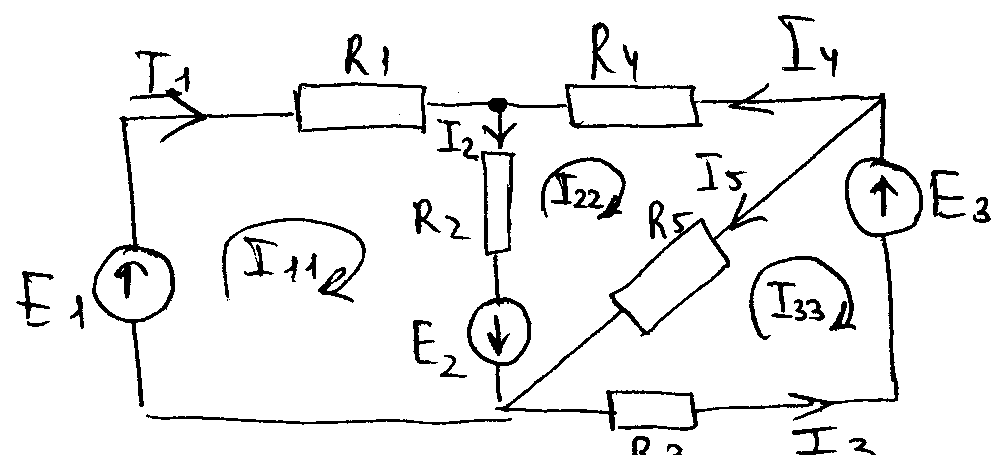
3 независимых контура, контурных уравнений будет 3. Для единообразия желательно, чтобы все контурные токи были направлены в одну сторону.

(*)

Систему (*) можно представить в матричном виде:

В общем случае, если электрическая цепь содержит N независимых контуров, то контурный ток в K-м контуре может быть найден по формуле:

, где

Δk – определитель матрицы, получаемый из матрицы [R] заменой k-го столбца на матрицу-столбец контурных ЭДС.

Последовательное и параллельное соединение сопротивлений в цепи постоянного тока (метод эквивалентных преобразований).

Если электрическая цепь содержит 1 источник ЭДС, можно применить МЭП и рассчитать электрическую цепь, используя закон Ома. Существуют 4 основных вида соединения элементов:

• Последовательное

• Параллельное

• Треугольник

• Звезда

(2) (**)

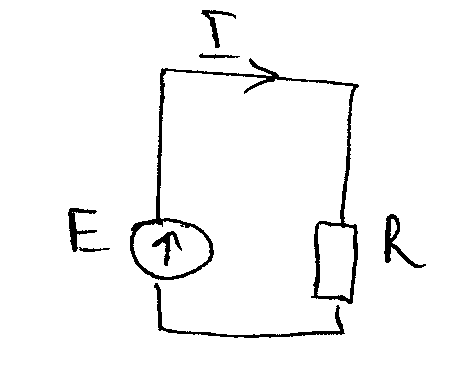
(1)

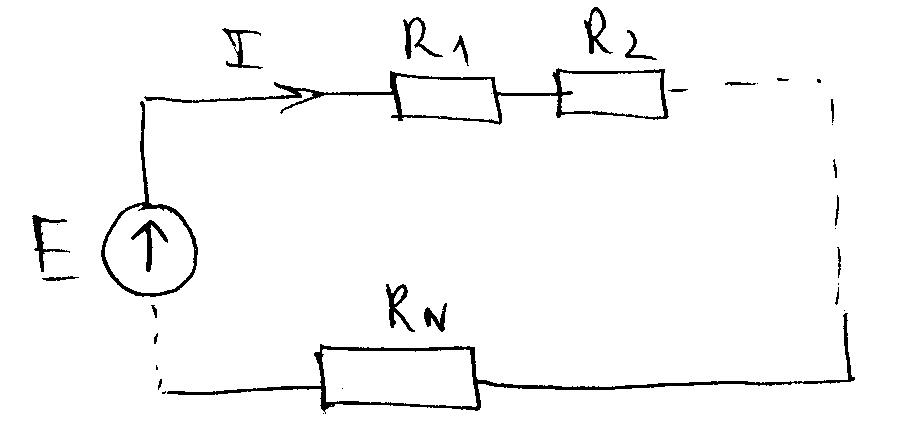
При последовательном соединении элементов через все элементы протекает один и тот же ток:

Для цепи (1) можно записать 2-й закон Кирхгофа:

IR₁+IR₂+…+IR_N=E

(R₁+R₂+…+R_N)I=E (*)

Эквивалентность понимается в смысле равенства токов в схеме (1) и (2).

Сравнивая (*) и (**): Rэк=R₁+R₂+…+R_N.

При последовательном соединении сопротивлений их эквивалентное сопротивление равно сумме отдельных сопротивлений.

Параллельное соединение – все элементы (сопротивления) подключаются к одной паре узлов.

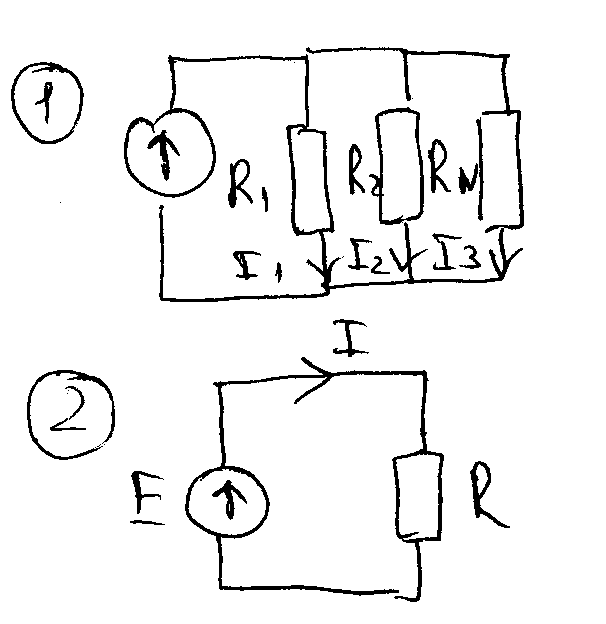
I=I₁+I₂+…I_N.

.

Сравнивая(*) и (**), получаем:

;

Так как суммарная (эквивалентная) проводимость не может быть меньше проводимости ветви с наименьшим сопротивлением при параллельном соединении сопротивлений, эквивалентное сопротивление всегда меньше сопротивления ветви с наименьшим сопротивлением.

Рассчитать токи I₁, I₂, I₃.