16.1. Векторное произведение векторов.
Векторным
произведением векторов
и
называется вектор
,
удовлетворяющий следующим условиям:1)
,
где
- угол между векторами
и
,
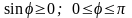
2) вектор ортогонален векторам и
3
)
,
и
образуют правую тройку векторов.Обозначается:
или
.
Свойства векторного произведения векторов:
1)
;2)
,
если
или
=
0 или
=
0;
3) (m ) = (m ) = m( );
4)
(
+
)
=
+
;
5)
Если заданы векторы
(xa,
ya,
za)
и
(xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
,
то
=
6)
Геометрическим смыслом векторного
произведения векторов является площадь
параллелограмма, построенного на
векторах
и
.
17.1. Смешанное произведение векторов и его свойства.
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где
a={ax,ay,az}
b={bx,by,bz}
c={cx,cy,cz}
Св-ва: 1. При перестановке 2х сомножителей:
a*b*c=-b*c*a
2. не меняется при перестановке циклических сомножителей:
a*b*c=c*a*b=b*c*a
3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0
б)если некомпланарные вектора a,b,c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах
если a*b*c>0, то тройка a,b,c - правая
если a*b*c<0, то тройка a,b,c - левая
1.1.Матрицы (основные понятия). Линейные операции над матрицами, их свойства
Матрицей наз прямоуг таблица чисел, содерж m-строк и n-столбцов. Матрицы равны между собой, если равны соответств элементы этих матриц. Матрица, в которой m=n наз квадратной или n-ого порядка. Квадр матрица, у которой все элементы, кроме элементов гл диагонали, равны 0 еаз диагональной. Диаг матрица, у которой каждый элемент главной диаг =1 наз единичной. Квадратная матрица наз треуг, если все элементы, расположенные по одну сторону её гл диаг =0. Матрица, у которой все числа, стоящие на гл диаг не нулевые, а также некоторое кол ненулевых строк, наз трапециевидной. Матрица, содерж один столбец или строку, наз вектором из Rn пр-ва. Действия. Сложение – только для матриц одинакового размера. Умножение на число. Множества матриц одинакового размера обознач Mm*n. Тогда введённое на этом мн-ве операции сложения и умнож на число превращ Mm*n в линейное пр-во, векторами которого явл матрицы m*n. Умножение на вектор-столбец. Для умножения матрицы на вектор-столбец надо, чтобы число столбцов матрицы было равно числу координат вектора. Две матрицы наз эквивалентными, если одна из них получена из другой с помощью эл. Преобраз. Любую матрицу можно привести к канонической.