39. Поле. Свойства поля

Определение. Коммутативное кольцо с единицей, содержащее не менее двух элементов, в котором любой отличный от нуля элемент обратим, называется полем.

Простейшие свойства поля

1. Т.к. поле — кольцо, то все свойства колец переносятся и на поле.

2. В поле нет делителей нуля ,т.е. если ab=0 ,то a=0 или b=0.

Доказательство.

Если a0 ,то  a^-1 . Рассмотрим a^-1 (ab)=( a^-1 a)b=0 , а если a0 ,то b=0, аналогично если b

3. Уравнение вида ax=b, a0, b – любое, в поле имеет единственное решение x= a^-1b, или х=b/a.

Решение этого уравнения называется частным.

Примеры.

1) PC, P — числовое поле.

2) P={0;1};

3) P={0;1;2} .

40. Характеристика поля

Не все свойства числовых полей сохраняются в случае произвольного поля. Так, складывая число 1 само с собою несколько раз, т.е. беря любое целое положительное кратное единицы, мы никогда не получим нуля. Если же мы будем брать целые кратные единицы в каком-либо конечном поле, то среди них непременно будут равные, т.к. это поле обладает лишь конечным числом различных элементов. Если все целые кратные единицы поля P являются различными элементами поля P, т.е. k1m1(здесь и далее за 1 обозначен элемент поля = единице) при km, то говорят, что поле P имеет характеристику нуль(char P=0);таковы, например, все числовые поля. Если существуют такие целые k и m, что k>m, но в P имеет место равенство k1=m1, то (k-m) 1=0, т.е. в P существует такое положительное кратное единицы, которое оказывается равным нулю. В этом случае P называется полем положительной характеристики. Характеристикой поля в случае поля положительной характеристики называют наименьшее натуральное р, что единица сложенная р раз дает 0.

Cвойства характеристики

1) Если char P=p>0, то p — простое число.

Доказательство (от противного).

Пусть p не простое число, а составное, т.е. p=ns, n>1,s>1 . Сложим единицу p раз: p1=(n1)·( s1)=0 n○1=0 либо s○1=0. Ибо в поле нет делителей нуля, но n<p и s<p. Противоречие с выбором числа p.

2) ap =0,  aP .

Любой элемент поля, сложенный р раз, где p — характеристика, равен нулю.

Доказательство:

ap= =a = a(p1)=a×0=0

41. Конечные кольца и поля.

Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов.

Конечное поле обычно обозначается   или GF(q), где q — число элементов поля.

Простейшим примером конечного поля является   — кольцо вычетов по модулю простого числа p.

Характеристика конечного поля является простым числом.

• Число элементов любого конечного поля есть его характеристика в натуральной степени:  .

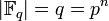• Для каждого простого числа p и натурального n существует конечное поле из q = pⁿ элементов, единственное с точностью до изоморфизма. Это поле изоморфно полю разложениямногочлена  .

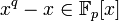• Мультипликативная группа 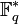  конечного поля   является циклической группой порядка q − 1.

  • В частности, в конечном поле всегда существует примитивный элемент α, порядок которого равен q − 1, то есть α^{q − 1} = 1 и 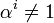  для 0 < i < q − 1.

  • Любой ненулевой элемент β является некоторой степенью примитивного элемента:

.

• Поле 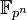  содержит в себе в качестве подполя 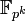  тогда и только тогда, когда k является делителем n.

• , где p — простое: 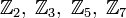  и так дале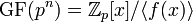е.

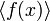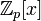• , где   — главный идеал кольца  , порожденный неприводимым многочленом 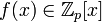  степени n.