Нахождение обратной матрицы

1. Метод присоединенной матрицы

1.

2.

3.

3.1 (взаимная)

3.2

4.

5.

2. Метод элементарных преобразований

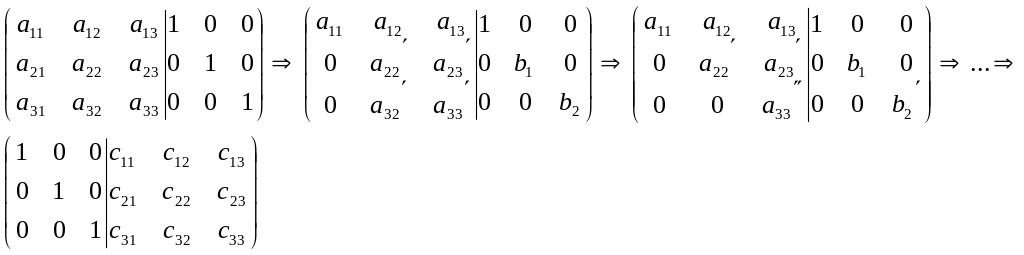
Графы

Графом называется двуосновная модель <V, E; i >, где i – бинарное отношение множеств V и E, такое, что каждый элемент e О E находится в отношении i либо ровно с одним, либо ровно с двумя элементами множества V.

При этом элементы множества V называются вершинами графа, элементы множества E называются рёбрами графа, а отношение i – отношением инцидентности. Вершины, инцидентные одному и тому же ребру, называются смежными.

Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра – линиями, соединяющими те точки, соответствующим вершинам которых ребра инцидентны.

Если ребро инцидентно только одной вершине, его называют петлей. Рёбра называются кратными, если они инцидентны одним и тем же вершинам.

Граф без кратных рёбер и петель называется простым графом.

Способы задания графа:

• Явное задание графа как алгебраической системы.

• Геометрический

• Матрица смежности

• Матрица инцидентности

Степенью вершины назовём удвоенное количество петель, инцидентных этой вершине плюс количество остальных инцидентных ей рёбер.

Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).

Подграфом, порождённым множеством вершин U называется подграф, множество вершин которого – U, содержащий те и только те рёбра, оба конца которых входят в U.

Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.

Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины смежны.

Маршрутом в графе называется чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершинами, такую, что каждое ребро в нем соединяет только те вершины, между которыми оно стоит.

Будем говорить, что этот маршрут соединяет первую и последнюю вершину. Если существует маршрут, то последняя вершина называется достижимой из первой вершины.

Маршрут, в котором нет повторяющихся ребер, называется цепью.

Маршрут, в котором нет повторяющихся вершин (кроме первой и последней), называется простой цепью.

Если в простой цепи первая и последняя вершины совпадают, то она называется циклом.

Граф называется связным, если любая вершина достижима из любой другой вершины. В противном случае граф называется несвязным. Несвязный граф распадается на несколько частей, каждая из которых является связным графом.

Эти части называются компонентами связности.

Ребро называется циклическим, если оно входит хотя бы в один цикл графа. В противном случае ребро называется ациклическим.

Связными компонентами графа называются подграфы данного графа, вершины которых являются классами эквивалентности отношения свзанности в данном графе.

Цикломатическим числом графа называется число связных компонент графа плюс число рёбер минус число вершин.

Эйлеровым называется цикл, проходящий по каждому ребру графа ровно один раз. Граф, имеющий эйлеров цикл, тоже будем называть эйлеровым.

Гамильтоновым называется цикл, проходящий по каждой вершине графа ровно один раз.

Связный граф без циклов называется деревом

Граф без циклов называется лесом. Вершины степени 1 в дереве называются листьями.

Гранью графа, изображенного на некоторой поверхности, называется часть поверхности, ограниченная рёбрами графа.

Плоский граф Существует правило изображение графов на поверхности: рёбра графа должны пересекаться только своими концами, то есть в точках, представляющих вершины графа.

Граф, вершинами которого являются грани графа G, изображенного на поверхности, рёбрами – рёбра графа G, гранями – вершины графа G, отношение инцидентности – отношением ограниченности графа G, а отношение ограниченности – отношением инцидентности графа G, называется двойственным графом к графу G.

24