3. Матрицы в теории устойчивости сооружений.
Определение критических сил в рамах методом А.Ф.Смирнова.
Рассмотрим определение перемещений по формуле Мора в матричной форме в случае узлового нагружения рам сосредоточенными силами. Деформации такой рамы после потери устойчивости показаны на Рис.3.1:
Рис.3.1.
Схема потери устойчивости рамы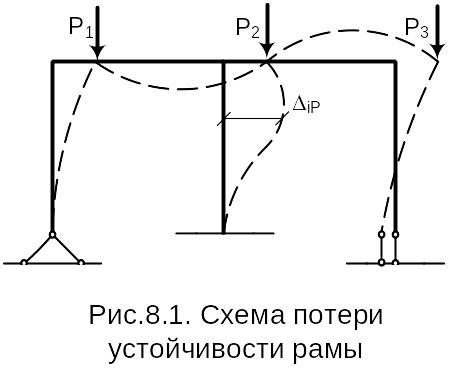
(3.1)
В
формуле (3.1)
изгибающий момент от единичной силы,
направленной также как определяемое
перемещение. G*
– матрица податливости системы, вид
которой рассмотрим позже. MP
–
матрица изгибающих моментов от
заданной нагрузки. При узловой передаче
внешней нагрузки изгибающие моменты в
элементах рамы будут выражены через
параметр нагрузки и поперечные
перемещения:
(3.2)
где
- критический параметр, U
–
матрица раскрытия статической
неопределимости (2.10), Н
– некоторая числовая матрица,
- вектор поперечных перемещений точек
рамы. После подстановки (3.2) в (3.1) получим
выражение:
Выбрав в качестве точек «i» те же точки, что при построении матрицы , окончательно получаем:
,
(3.3)
где
- матрица раскрытия статической
неопределимости (2.10):
.
В
формуле
- матрица изгибающих моментов от единичных
значений неизвестных Хi
= 1 метода сил. G
– матрица податливости, состоящая
из блоков
В
формуле (3.3)
-
матрица изгибающих моментов от единичных
сил, прикладываемых по направлению
определяемых перемещений системы.
Обозначим
(3.4)
Подставим (3.4) в (3.3), получим
(3.5)
Формула
(3.5) показывает, что
и
есть собственное значение и собственный
вектор матрицы С.
Рассмотрим формирование матрицы податливости G*. Матрица податливости всей системы формируется из матриц податливости отдельных участков и имеет следующую структуру
G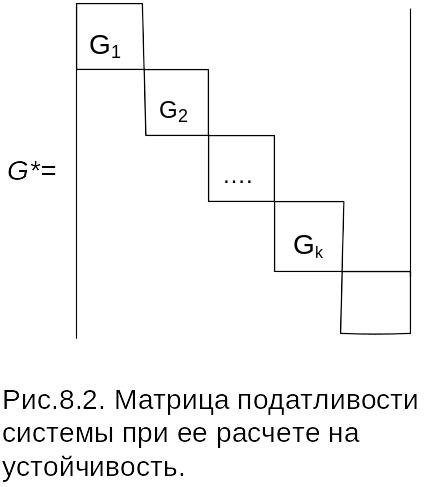
k
– блок
матрицы на k-ом
участке.
Вид матрицы Gk зависит от типа участка (какую деформацию он испытывает).
Рис.3.2.
Матрица податливости системы
при ее расчете на
устойчивость
1)Участок, испытывающий только изгиб
G=
,
(3.6)
где : l0-длина любого участка ,принятого за основной, B0-жесткость любого участка ,принятого за основную.
;
2)Участки, испытывающие деформацию сжатие с изгибом. Для такого участка вид матрицы Gk зависит от того на сколько панелей разбита его длина.
а) Длина участка разбита на две панели:
-длина
участка,
-длина
панели
;
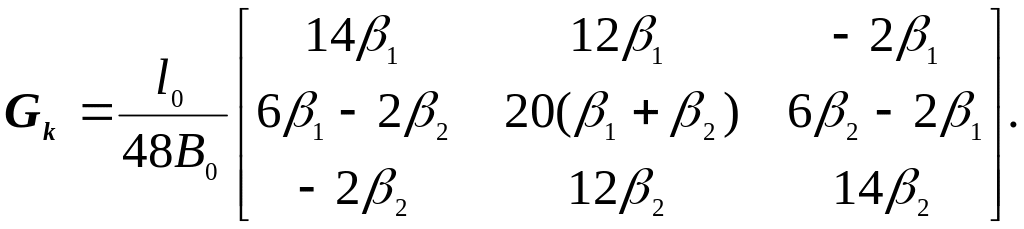(3.7)
б) Длина участка разбита на три панели:
;
;
.
(3.8)
в
)
Длина участка разбита на четыре и более
панелей:
В
этом случае общая длина сжато-изогнутого
элемента компонуется из подучастков с
двумя или тремя панелями.
Соответственно
компонуется матрица податливости
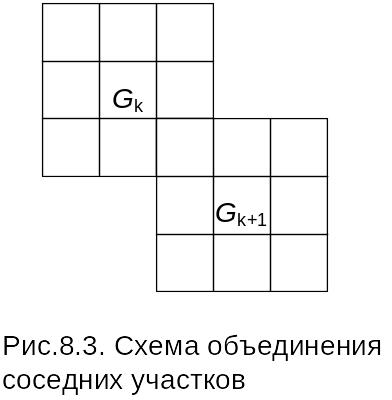(Рис.3.3).
Рис.3.3.
Схема объединения соседних
участков
Формирование матрицы H.
Матрица
H-числовая
матрица размером (μ×m),
преобразующая вектор перемещений
в эпюру моментов грузового состояния.
;
Для построения матрицы H необходимо определить изгибающие моменты во всех расчетных сечениях основной системы от узловых нагрузок и построить эпюру М0
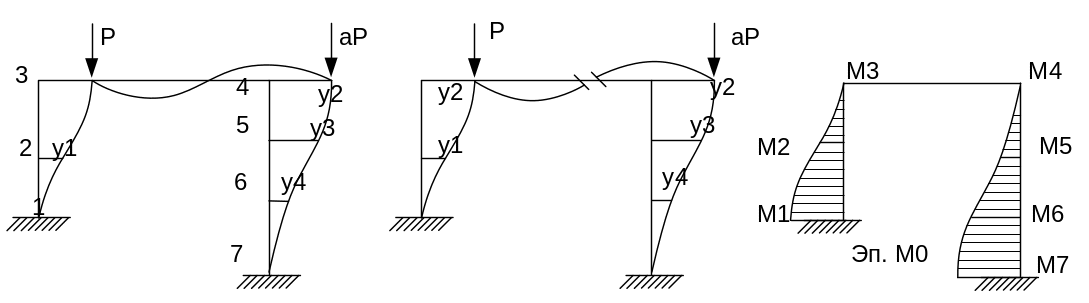
Рис.3.4. Схема для построения матрицы H
Эпюра М0 строится со стороны растянутых волокон с учетом деформированного состояния системы.
,
,
,
,
,
,
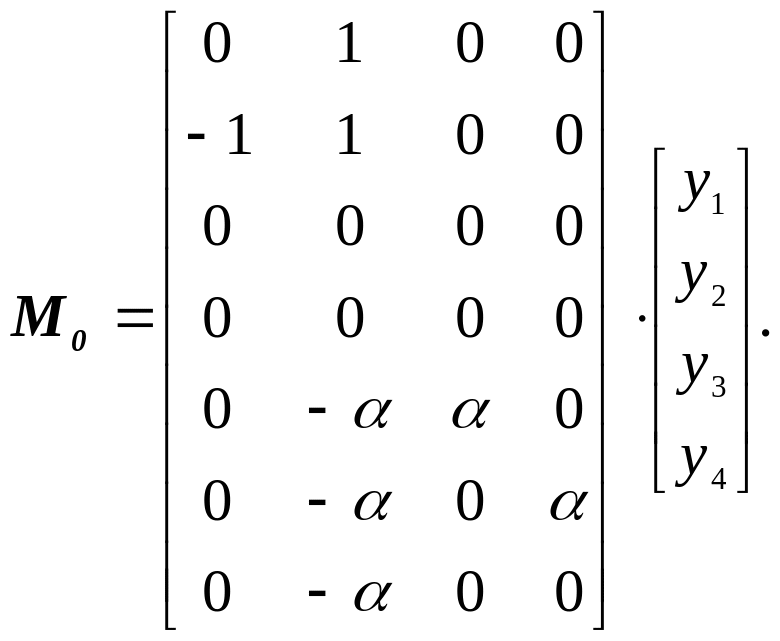
В матрицу H вписываются коэффициенты при перемещениях из каждого уравнения.
Пример №14. Найти критическую нагрузку для рамы, показанной на
Рис.3.5.
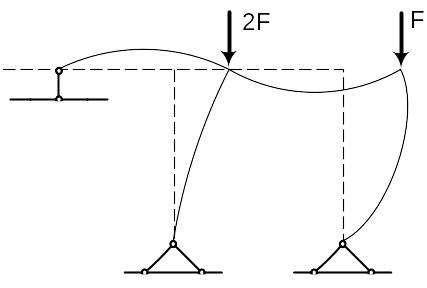
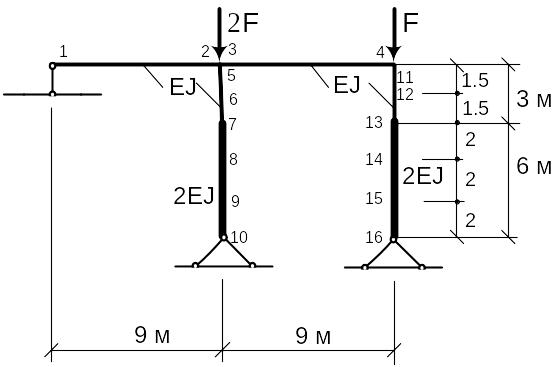Рис.3.6.
Форма потери
устойчивости рамы.
Рис.3.5. К примеру №14
Для составления матрицы податливости разобьем раму на участки. На Рис.3.5. показаны сечения на границах участков. Коэффициенты, входящие в блоки матриц податливости G и G*, приведены ниже:
;
;
;
;
;
.
Матрица податливости G участвует в вычислениях матрицы U:
Матрицу податливости G* формируем, используя (3.6) – (3.8)
Выберем основную систему и построим единичные эпюры М1 и М2
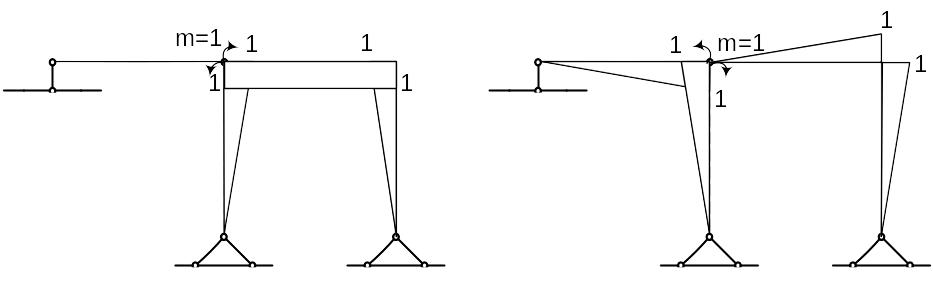
Рис.3.7. Эпюра М2. Рис.3.8. Эпюра М1.
Составим
матрицу
:
;
По формуле (2.10) вычисляем матрицу U.
Для составления матрицы Н покажем основную систему в деформированном состоянии и вычислим изгибающие моменты в сечениях рамы
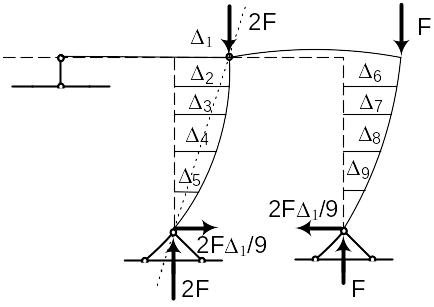
Рис.3.9. Основная система в деформированном состоянии
;
;
;
;
;
;
;
;
;
.
Формируем матрицу
,
где
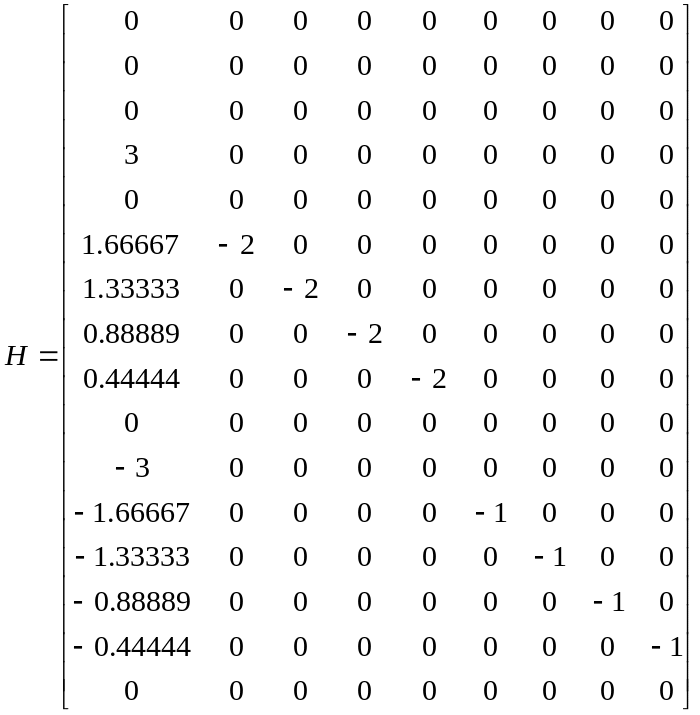
Строим единичные эпюры для определения перемещений (Рис.3.10).
Формируем
матрицу
:
Рис.3.10.
Единичные эпюры для определения
перемещений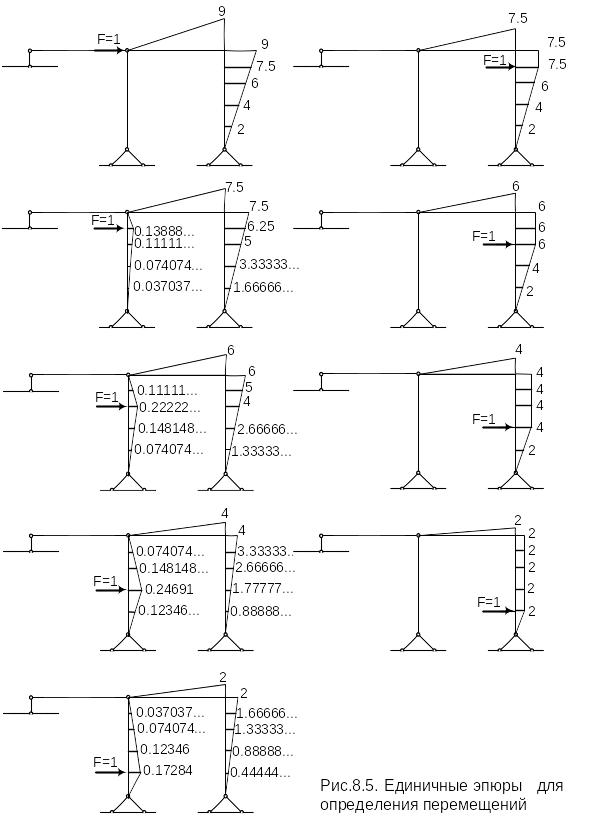
Перемножаем матрицы по формуле (3.4), получаем
.
Методом итераций находим старшее собственное число и собственный вектор этой матрицы:
;
;
.
Для оценки точности расчета выберем другую основную систему, построим единичные эпюры от неизвестных метода сил
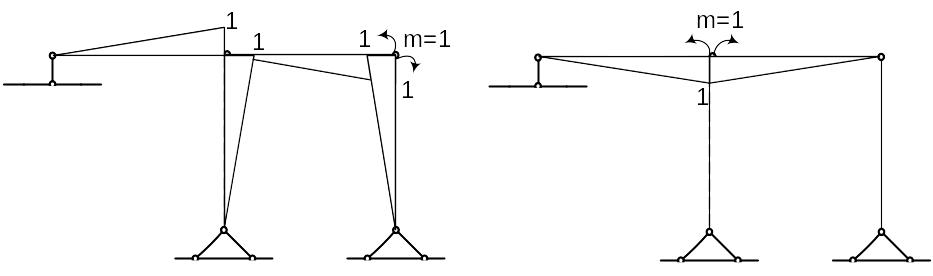
Рис.3.11. Эпюра М2 Рис.3.12. Эпюра М1.
Составим матрицу :
.
По формуле (2.10) вычисляем матрицу U, используя прежнюю матрицу G.
Для составления матрицы Н покажем основную систему в деформированном состоянии и вычислим изгибающие моменты в сечениях рамы
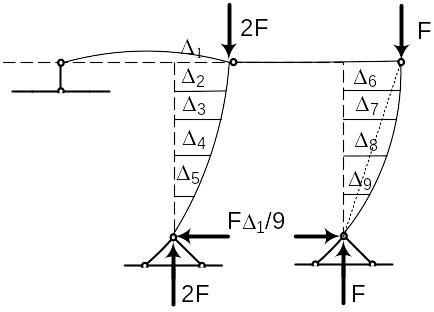
Рис.3.13. Основная система №2 в деформированном состоянии
;
;
;
;
;
;
;
;
;
.
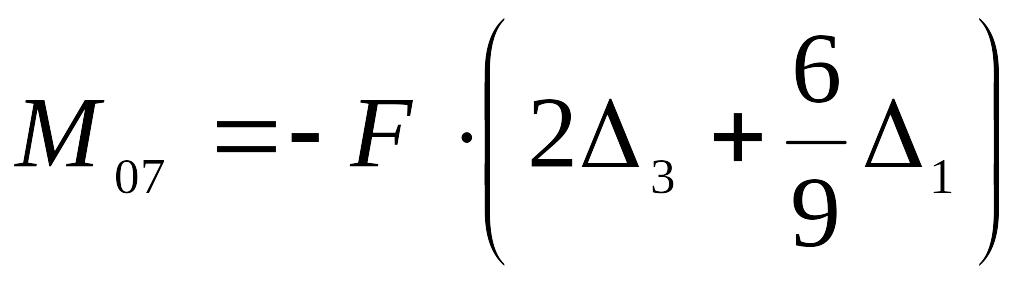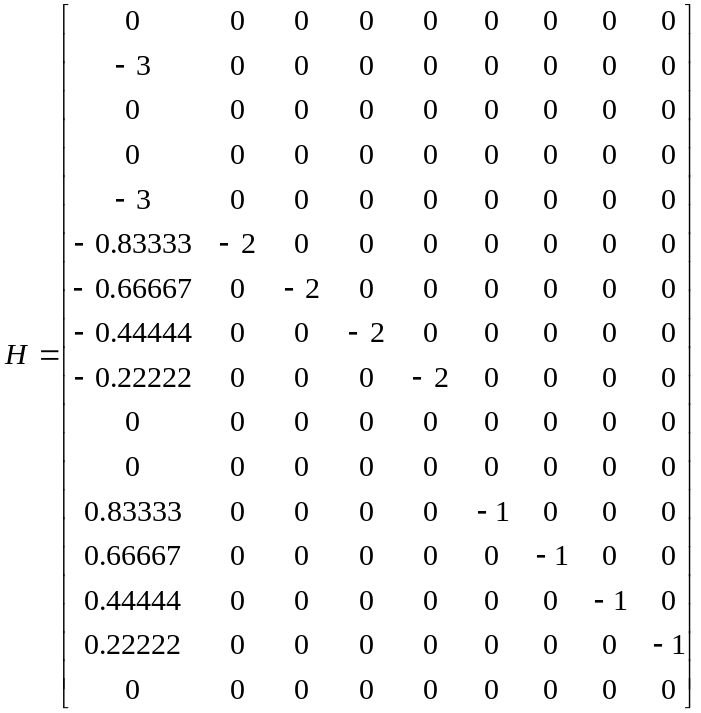
Формируем матрицу
,
Строим единичные эпюры для определения перемещений (Рис.3.14).
Рис3.14.
Единичные эпюры для определения
перемещений (2-й вариант основной
системы)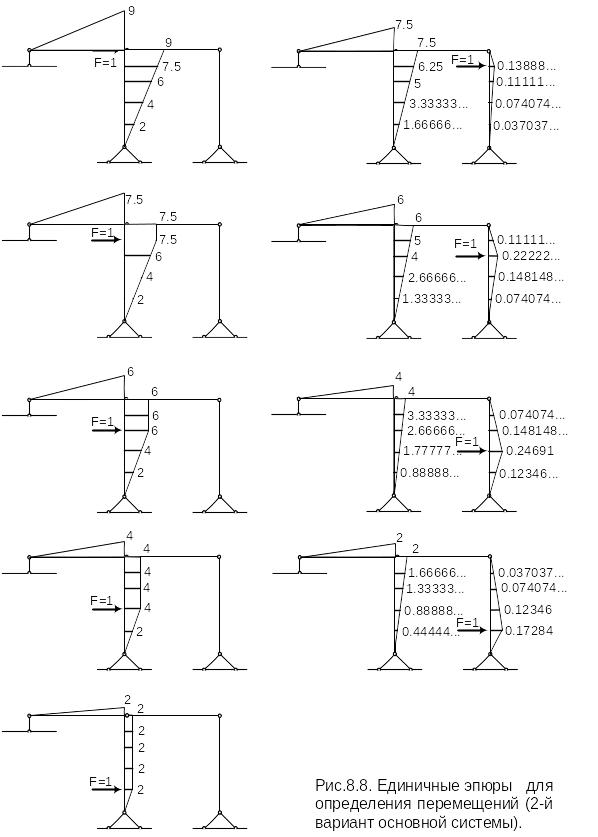
Формируем матрицу :
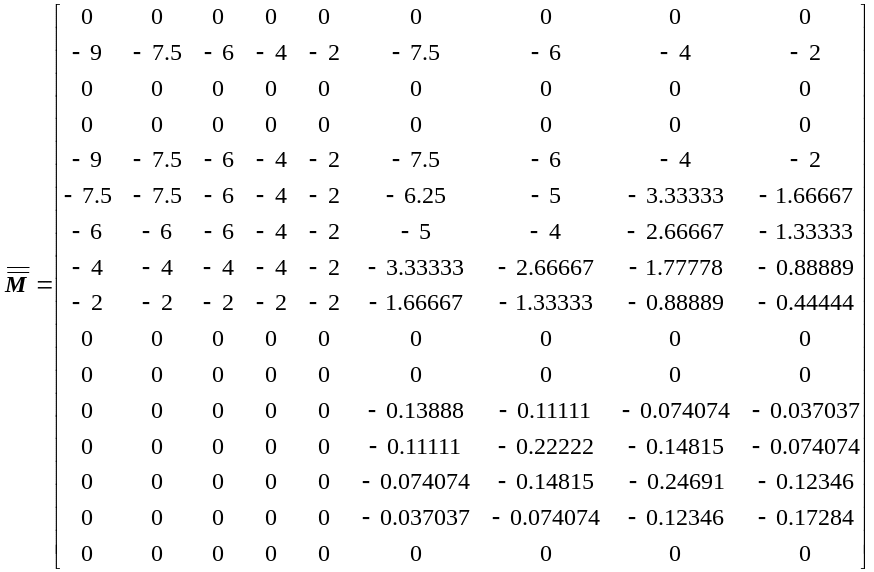
Перемножаем матрицы по формуле (3.4), находим
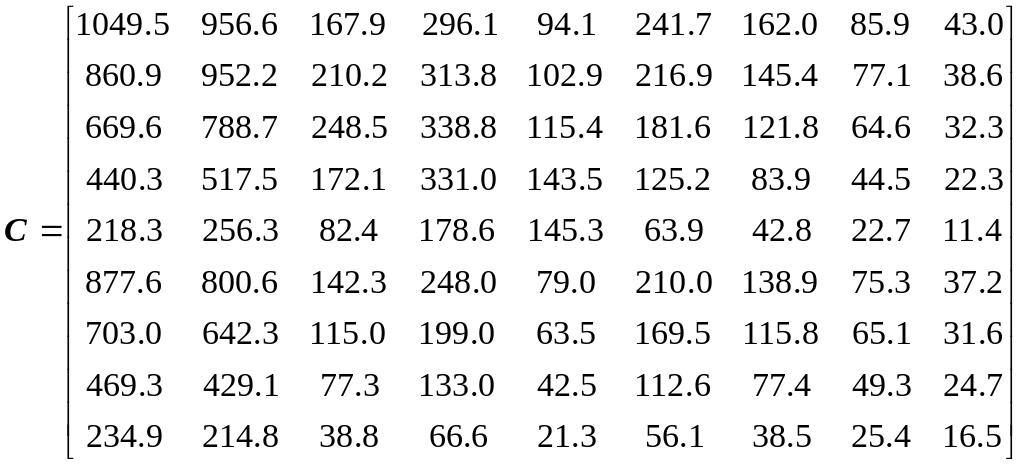
Методом итераций определяем старшее собственное число и собственный вектор этой матрицы:
;
;
.
Отличие от предыдущего значения составляет 3.65%, что показывает достаточно хорошую точность расчета.