1.2. Собственные числа и собственные векторы матриц

(1.1)

Если для квадратной матрицы A можно найти вектор и число , от­вечающие выражению (1.1), то этот вектор и это число называются собственным значением и собственным вектором матрицы A.

Решение (1.1) на первый взгляд несложно. В частности, из (1.1) сле­дует система линейных уравнений, коэффициенты которых выража­ются через элементы матрицы A и собственные числа :

(1.2)

Система однородных линейных уравнений (1.2) имеет ненулевое ре­шение в том случае, если определитель матрицы коэффициентов равен нулю:

. (1.3)

Для матрицы A – порядка n уравнение (1.3) есть алгебраическое урав­нение степени n, решив которое можно найти n собственных чисел , i=1,2,…..n, после их подстановки в (1.3) и решения n систем однородных линейных уравнений n – го порядка можно получить n – собственных век­торов.

Пример №6:

Дано:

Найти: собственные числа собственные векторы

Решение: составим характеристическое уравнение (1.3):

Корни этого уравнения есть собственные числа мат­рицы А: , . Находим собственные векторы, подставив значение в (1.2):

,

откуда , из условия нормирования находим , . Аналогично находим компоненты второго собственного век­тора, после подстановки в (1.2) :

,

откуда , из условия нормирования находим , .

Таким образом, найдены матрицы собственных значений , и собственных векторов .

Из изложенного выше следует, что описанный метод хорош только для матриц невысокого порядка и приводит к существенным вычислитель­ным трудностям при больших n.

Для матриц высокого порядка очень эффективен способ итераций, который состоит в следующем: задаются произвольным вектором , затем используют (1.1), проводя вычисления по схеме:

……… (1.4)

до тех пор, пока в пределах требуемой точности , не совпадут с , .

В (1.4) i это не номер собственного значения, а номер приближения для одного и того же собственного числа. Процесс (1.4) довольно быстро сходится к большему по величине собственному числу и к соответствую­щему ему собственному вектору. Следовательно, методом итераций можно найти только старшее собственное число.

Пример №7:

Дано:

Найти старшее собственное число соответствующий ему собствен­ный вектор.

Решение: зададим нормальный вектор: 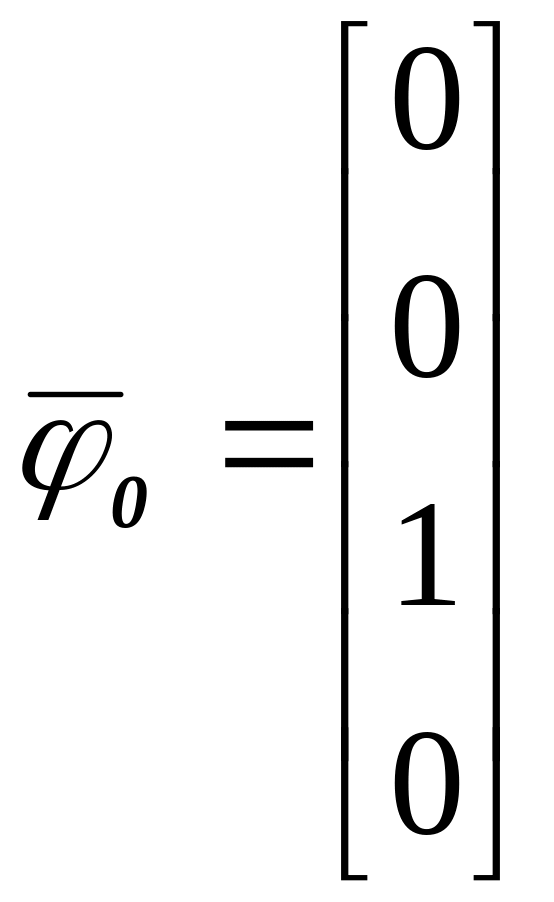после чего действуем по (1.4).

После первой итерации находим

92,504053965=

После второй итерации:

.

…………………………………………………………………………………………

После четвертой итерации: , .

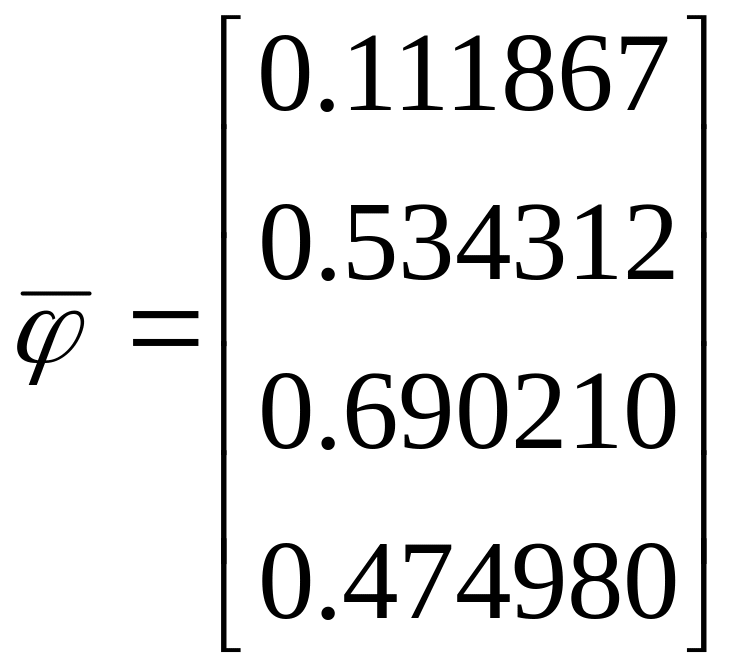1.3. Полная проблема собственных значений. Метод итераций.

Простота и легкость программирования метода итераций для опреде­ления старшего собственного числа объясняет стремление приме­нить этот метод к определению остальных собственных чисел, т.е. приме­нить метод итераций к решению полной проблемы собственных значений.

Равенство (1.1) записано для одного собственного числа. Матрич­ный аналог этого равенства выглядит следующим образом:

, (1.5)

где - диагональная матрица n – го порядка на главной диагонали кото­рой расположены собственные числа. матрица, составлен­ная из собственных векторов, записанных по столбцам.

Отметим очень важное свойство собственных векторов – свойство ортогональности: при . В матричной форме это условие запи­сывается так: где - диагональная матрица. Обычно нор­мируют собственные вектора: , тогда условие ортогонально­сти примет вид:

, (1.6)

где Е – единичная матрица.

Из (1.6) следует, что для нормированных собственных векторов

(1.7)

а также

(1.8)

В результате очередной итерации по формулам (1.4) получаем

(1.9)

где - нормированный , а – ненормированный вектор. Находим норми­рующий множитель

(1.10)

и затем нормированный вектор

(1.11)

Отсюда имеем

(1.12)

Сравнивая с (1.4), замечаем, что нормирующий множитель после оче­редной итерации

_i = . (1.13)

В (1.9) –(1.13) i – номер итерации, а не номер собственного числа.

С учетом (1.7) выражение (1.5) можно записать в виде:

(1.14)

Переходя к векторной форме записи, получим:

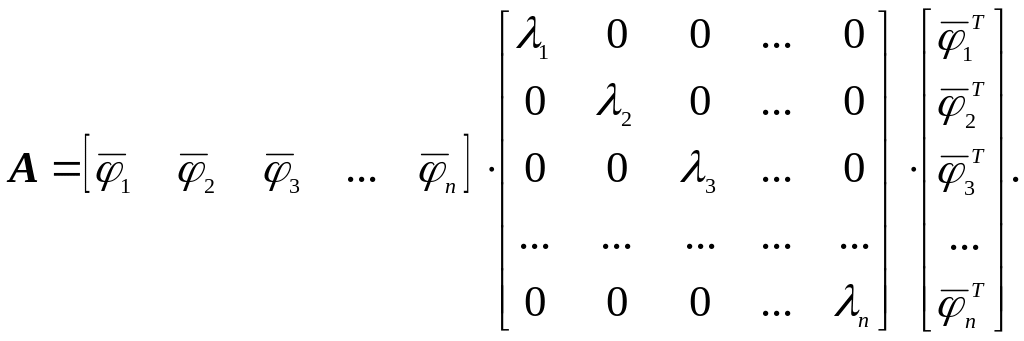
После перемножения матриц в правой части, имеем:

(1.15)

Обозначим

. (1.16)

Тогда

,

, (1.17)

…………………………………………

,

Применим к (1.17) метод итераций и найдем старшие собственные числа и собственные векторы матриц A_i . Здесь i – номер собственной формы. Предполагаем, что правые части (1.15), (1.17) записаны в порядке убывания собственных чисел. Тогда из A_i методом итераций находится и .

Таким образом, имеем следующую схему решения полной проблемы собственных значений матрицы A:

а) методом итераций из A находим , по формулам (1.9) – (1.13)

б) по (1.16) определяем A₁,

в) методом итераций из A₁ находим и ,

г) по (1.16) определяем A₂,

и т.д. повторяем процесс, пока не найдем все n собственных чисел.

Пример №8. Найти все собственные векторы и собственные числа матрицы

Применяем, описанный выше метод итераций к матрице А. Вычисления велись на ПК в программе Excel.

Находим 139.658735, 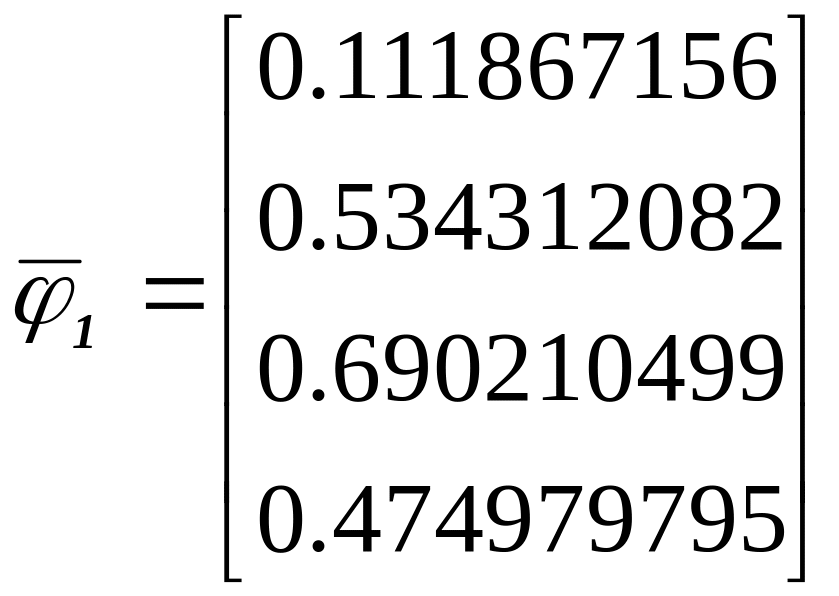. По формуле (1.16) вычисляем

Применив метод итераций к А₁, находим

= 18,03255539, .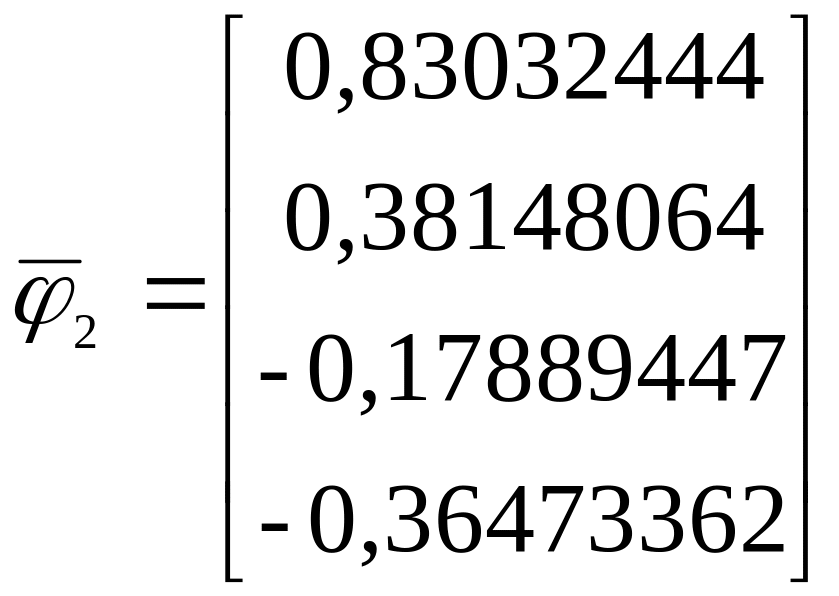

По формуле (1.16) вычисляем

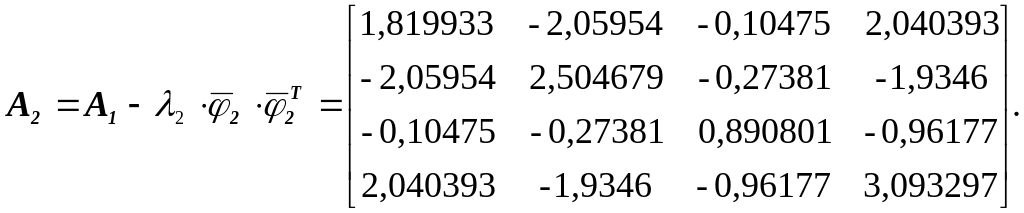
Применив метод итераций к А₂, находим

= 6,577921363, .

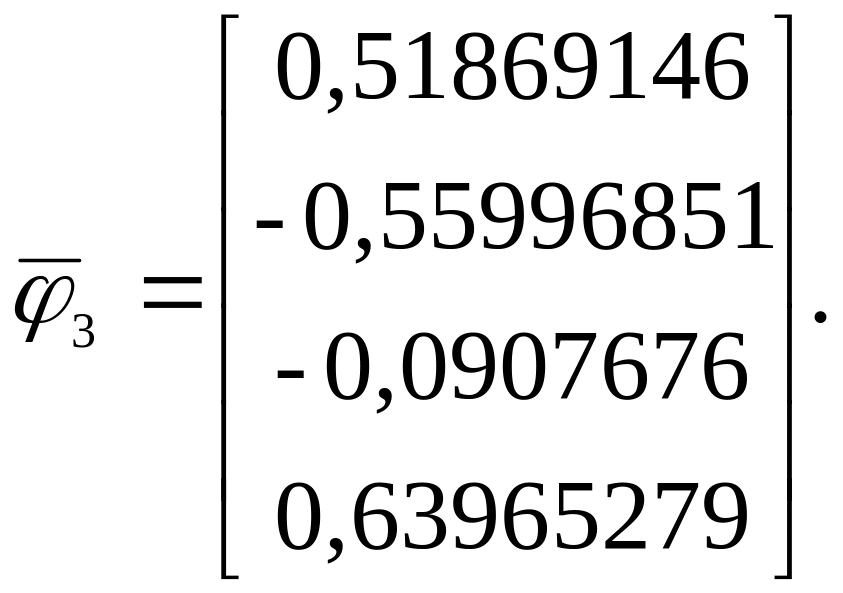По формуле (1.16) вычисляем

Применив метод итераций к А₃, находим

= 1,730788224, .

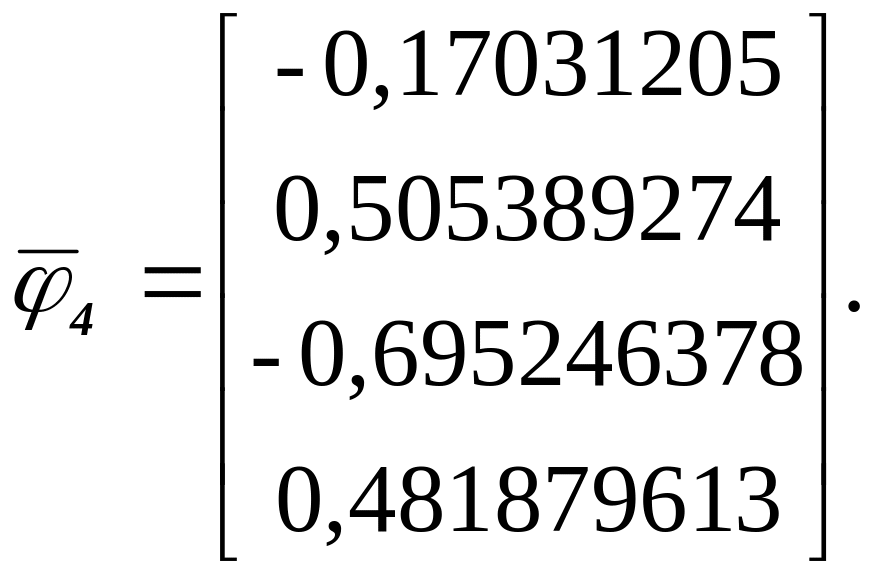Применив еще раз формулу (1.16), находим

Элементы матрицы А₄ , которые должны бать равны нулю, позволяют оценить точность расчетов. Как видно, погрешность имеет порядок 10^-12, что очень хорошо, если учесть значения элементов матрицы А₃ , имею­щие порядок 10^-0.