9. Постоянный электрический ток. Осн. Хар-тики эл тока. Эдс и напряжение. Закон Ома для однородного участка цепи в интегр и диффер формах. Эл-ское сопротивление. Проводимость.

Э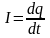 лектрическим током называется упорядоченное движение электрических зарядов. Сила тока I —скалярная физическая величина, равная отношению заряда dq, переносимого сквозь рассматриваемую поверхность за малый промежуток времени, к величине dt этого промежутка

Д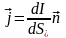 ля хар-ки направления эл тока в разных точках рассматриваемой поверхности и распределения силы тока по этой поверхности служит вектор плотности тока j

Условия существования электрического тока: 1) наличие свободных носителей тока — заряженных частиц, способных перемещаться упорядоченно;

2) наличие эл поля, энергия кот должна каким-то образом восполняться источником тока.

Ф 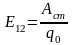из вел, определ работой, кот совершают сторонние силы при перемещении единичного положительного заряда на участке 1-2, называется электродвижущей силой (ЭДС) действующей в цепи на этом участке:

Н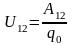 апряжением U на участке 1—2 наз физ вел, численно равная суммарной работе совершаемой электростатическ и сторонними силами по перемещ единичн положит заряда на данном участке цепи:

З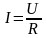 акон Ома в интегральной форме : сила тока, текущего по однородному металлическому проводнику, пропорциональна напряжению на концах проводника

К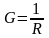 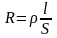оэффициент пропорциональности в законе Ома R называется электрическим сопротивлением проводника.

Электр. Проводимость – величина обратная сопростивлению:

З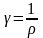 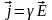акон Ома в дифференциальном виде для однородного участка

Где γ – удельная проводимость

1 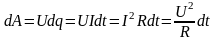0.Работа и мощность эл тока. Закон Джоуля-Ленца в интегральной и дифференциальной форме.

З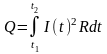 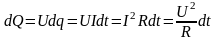акон Джоуля–Ленца в интегр форме: кол-во теплоты, выделяемое постоянным эл током на участке цепи, равно произвед квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.

У дельной тепловой мощностью тока w называется количество теплоты, выделяющееся за единицу времени в единице объема:

Это закон Джоуля – Ленца в диффер Форме.

11.Закон Ома для неоднородного участка цепи.Обобщенный закон Ома в интегр форме. Частные случаи. Правила Кирхгофа для расчета разветвленных цепей.

З 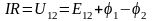акон Ома для неоднородного участка цепи в интегральной форме является обобщенным законом Ома:

Ч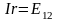 астные случаи. Закон Ома для замкнутой цепи:

С лучай короткого замыкания: , R=0

З акон Ома для однородного участка цепи:

ЭДС, действующая в разомкнутой цепи

1 правило Кирхгофа

2 правило Кирхгофа

12. Классическая теория электропроводности металлов. Плотность тока. Законы Ома и Джоуля-Ленца. Трудности классической теории.

С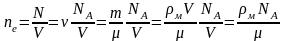 огласно теории Друде–Лоренца, электроны в металлах образуя электронный газ, обладающий свойствами идеального газа и обладают той же энергией теплового движения, что и молекулы одноатомного газа.

Д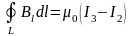 рейфовая скорость электрона в металле: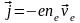

К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию, которая при соударении электрона с ионом полностью передается решетке.

<E_k>=m_ev²_max/2=e²λ²/(2m_eu²_кв);

ω=z<E_k>n_e(u_кв/λ)·<E_k>=e²λn_e/(2m_eu²_кв)E²=γE², где

Трудности классической теории.

1 ) Оценка среднего пробега электронов. Чтобы получить величины удельной проводимости, совпадающие с опытными данными, следует принимать значение длины пробега в сотни раз больше межатомных расстояний в кристалле.

2 ) <u_кв>~корень(T);

γ~<u_кв>^-1~1/корень(T);

ρ~корень(T), но

ρ=ρ₀αT.

3) Теплоёмкость металла складывается из теплоемкости кристаллической решетки и теплоемкости электронного газа. Поэтому удельная теплоемкость металла должна быть существенно выше теплоемкости диэлектриков, у которых нет свободных электронов, что противоречит эксперименту.

З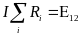 акон Ома для неоднородного участка цепи в интегральной форме является обобщенным законом Ома:

Закон Ома для однородного участка цепи:

З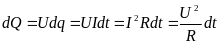 акон Джоуля–Ленца в интегр форме: кол-во теплоты, выделяемое постоянным эл током на участке цепи, равно произвед квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.

У дельной тепловой мощностью тока w называется количество теплоты, выделяющееся за единицу времени в единице объема:

Это закон Джоуля – Ленца в диффер Форме.