3.5. Пропускная способность непрерывного канала. Теорема Шеннона

Пропускная способность непрерывного канала в расчете на один отсчет передаваемого сигнала, по аналогии с формулой (1.24а), определяется как

.

(3.49)

Здесь Х и Y - случайные величины, отсчеты процессов X(t) и Y(t) на входе и выходе канала. Пропускная способность С определяется как сумма значений С_отсч, взятая по всем отсчетам за секунду. При этом дифференциальные энтропии в (3.49) должны вычисляться с учетом вероятностных связей между отсчетами. Вычислим пропускную способность непрерывного канала без памяти с аддитивным белым (т.е. имеющим равномерный энергетический спектр и полностью некоррелированные несовпадающие отсчеты) гаусовском шумом, имеющим полосу пропускания F, если средняя мощность сигнала (дисперсия Х) не превышает заданной величины Р_с. Мощность (дисперсию) шума в полосе F обозначим Р_ш. Поскольку шум аддитивный, отсчеты входного Х и выходного Y сигналов и шума N связаны равенством

Y=X+N,

(3.50)

т.к. N имеет нормальное распределение с нулевым математическим ожиданием, то и условная плотность вероятности (у/x) при фиксированном х будет также нормальной с математическим ожиданием х и дисперсией Р_ш. Найдем пропускную способность в расчете на один отсчет (3.49):

.

Дифференциальная энтропия гауссовского распределения h(Y/X) в соответствии со своим свойством 2 (§ 3.3) не зависит от математического ожидания и согласно (3.37) равна . Поэтому для определения С_отсч следует найти такую плотность распределения (x), при которой максимизируется h(Y). Из (3.50) учитывая, что X и N-независимые случайные величины, имеем для дисперсий:

D(Y)=D(X)+D(N)=Pc+Pш,

(3.51)

таким образом, дисперсия Y фиксирована, так как Р_с и Р_ш заданы. В соответствии со свойством 4 дифференциальной энтропии (§ 3.3) максимальная дифференциальная энтропия при фиксированной дисперсии обеспечивается гауссовским распределением. Из (3.50) видно, что при нормальном распределении Х распределение Y будет также нормальным и, следовательно, обеспечивается максимум дифференциальной энтропии (4.37):

,

откуда . Переходя к пропускной способности С в расчете на секунду, заметим, что количество информации, содержащейся в следующих друг за другом отсчетах, максимально в том случае, когда отсчеты независимы. Этого можно достичь, если процесс X(t) выбрать таким, чтобы его спектральная плотность была равномерной в полосе частот F. В этом случае отсчеты, разделенные интервалами t, кратными 1/(2F), взаимно некоррелированы, а для гауссовских величин некоррелированность означает независимость. Поэтому пропускную способность С (за секунду) можно найти, сложив пропускные способности (3.52) для 2F независимых отсчетов:

.

(3.53)

Она реализуется, если X(t) - гауссовский процесс с равномерной спектральной плотностью в полосе частот F (квазибелый шум). Соотношение (3.53) называют формулой Шеннона. Формула Шеннона указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. Однако поскольку С зависит от F линейно, а от Р_с/P_ш – по логарифмическому закону, компенсировать возможное сокращение полосы пропускания увеличением мощности сигнала, как правило, не выгодно. Более эффективным является обратный обмен мощности сигнала на полосу пропускания. Рассмотрим, как меняется пропускная способность гауссовского канала с изменением полосы пропускания. Для этого выразим мощность шума в канале через его одностороннюю спектральную плотность N₀. Имеем Р_ш=N₀ F, поэтому

.

(3.54)

При увеличении F пропускная способность С сначала быстро возрастает, а затем асимптотически стремиться к пределу

.

(3.55)

Результат (3.55) можно получить, если учесть, что при  <<1 (т.е. при больших F) ln(1+). Зависимость С_ от F показана на рисунке. И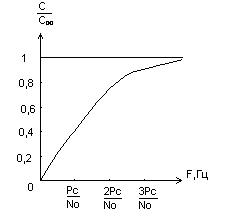 сходя из (3.55) можно показать, что для передачи заданного количества информации по каналу с шумом отношение энергии сигнала к спектральной плотности шума должно превысить некоторую пороговую величину. Действительно, если на передачу сообщения затрачено время Т, то среднее количество переданной информации , т.к. пропускная способность канала при любой полосе F не может превысить предельное значение (3.55). Таким образом и, следовательно, для передачи одного бита (т.е. ) информации необходима энергия сигнала

.

Эти рассуждения устанавливают потенциально взаимосвязь между количеством переносимой сигналом информации и энергией сигнала. Отметим, что формула Шеннона (3.53) справедлива только для канала с постоянными параметрами и аддитивным гауссовским белым или квазибелым шумом. Если аддитивный шум не гауссовский и его спектр неравномерен в полосе пропускания канала, то его пропускная способность больше, чем вычисленная по формуле (3.53). Мультипликативные помехи (замирание сигнала), обычно снижают пропускную способность по сравнению с результатом (3.53). Рассмотрим теперь вопрос согласования источника непрерывных сообщений с непрерывным каналом. Передача непрерывных сообщений по каналу без помех не представляет интереса, так как в этом теоретическом случае проблема связи вообще не возникает. Одним импульсом, амплитуда которого на приемной стороне воспринимается с неограниченной точностью, может быть передано бесконечно большое количество информации, однако этот результат не может быть использован в практике, так как этот импульс нельзя точно измерить. Для канала с шумом с пропускной способностью С, на вход которого подключен источник с производительностью Шеннон доказал следующую теорему. Если при заданном критерии эквивалентности сообщений источника его e-производительность меньше пропускной способности канала , то существует способ кодирования и декодирования, при котором неточность воспроизведения сколь угодно близка к (прямая теорема). При такого способа не существует (обратная теорема). Доказательство теоремы осуществляется аналогично доказательству основной теоремы кодирования для канала с шумом. Термин «кодирование» здесь понимается в широком смысле, так как он определен во введении. Не доказывая теорему, поясним возможность осуществления указанного в ней способа передачи. Если сообщения должны воспроизводиться с определенной верностью, то из бесконечного множества непрерывных сообщений длительностью Т передавать необходимо только конечное подмножество воспроизводящих сообщений. Процесс кодирования при этом заключается в отождествлении полученного от источника сообщения с ближайшим воспроизводящим и сопоставлением ему конкретного сигнала из множества разрешенных сигналов, специально подобранных для передачи, с учетом действующей в канале помехи. При декодировании полученный сигнал отождествляется с ближайшим разрешенным и ставится в соответствие воспроизводящему сообщению. Ошибки не произойдет, если при принятый сигнал попадет в некоторою собственную область соответствующего разрешенного сигнала, размеры которой зависят от средней мощности помехи. При определенном уровне средней мощности передаваемых сигналов можно создать ограниченное число разрешенных сигналов с не перекрывающимися собственными областями. Оно (это число) и определяет предельную скорость передачи с обеспечением заданного уровня верности. Поскольку обычно допускается возможность появления любого значения помехи, вероятность воспроизведения другого разрешенного сигнала остается конечной. Однако при доказательстве теоремы показано, что она стремится к нулю при неограниченном увеличении длительности передаваемых сигналов. При этом из теоремы Шеннона следует, что при выполнении условия , можно преобразовать сообщение в сигнал так, чтобы отношение сигнал-шум на выходе приемника (декодера) было больше значения ₀, обеспечивающего эквивалентность переданного и принятого сообщений, хотя в канале (т.е. на входе приемника) отношение сигнал-шум может быть во много раз меньше ₀. Однако до сих пор оптимальное кодирование непрерывных сообщений (без преобразования в дискретные) в непрерывном канале не находит приемлемой реализации. Более предпочтительным в настоящее время представляется преобразование непрерывных сообщений в дискретные с последующим использованием эффективного и помехоустойчивого кодирования.

48