
- •1 Фигура, диаметр, мера. Определённый интеграл по фигуре (определение)
- •2 Масса фигуры переменной плотности
- •3 Геометрический смысл ди (двойного интеграла)
- •4 Геометрический смысл Кр и -1
- •5 Свойства определённого интеграла по фигуре
- •6 Вычисление криволинейного интеграла 1-ого рода
- •7 Вычисление ди в декартовых координатах
- •8 Вычисление ди в полярных координатах
- •9 Вычисление тройного интеграла в декартовых координатах
- •10 Вычисление Тройного интеграла в цилиндрических координатах
- •11 Вычисление тройного интеграла в сферических координатах
- •12 Вычисление пи-1
- •13 Вычисление статических моментов фигуры
- •14 Вычисление координат центра тяжести фигуры
- •15 Вычисление моментов инерции фигуры
- •Связь между криволинейными интегралами 1 и 2 рода.
- •17 Формула Грина
- •18 Независимость Кр и-2 от пути интегрирования
- •20. Формула Стокса
- •21 Формула Остроградского-Гаусса
- •22. Скалярное поле. Линии и поверхности уровня скалярного поля. Производная по направлению.
- •23 Градиент, свойства градиента
- •24 Векторное поле, определение, векторные линии, труба
- •25 Поток векторного поля, его физический смысл
- •26 Дивергенция векторного поля, её свойства
- •27 Циркуляция векторного поля, её физический смысл
- •28 Ротор векторного поля, его свойства
- •29 Оператор Гамильтона, диф.Операции 1-го и 2-го порядка
- •30 Простейшие векторные поля: потенциальное, соленаидальное, гармоническое
- •31 Определение числового ряда, основные понятия. Необходимые и достаточные условия сходимости ряда
- •32 Свойства сходящихся числовых рядов
- •33 Необходимое условие сходимости ряда. Достаточное условие расходимости числового ряда
- •34 Признаки сравнения числовых рядов
- •35 Признак д'Аламбера
- •36 Радикальный признак Коши
- •37 Интегральный признак сходимости
- •38 Знакопеременные ряды. Абсолютная и условная сходимость. Достаточное условие абсолютной сходимости знакопеременного ряда
- •24.2. Абсолютная и условная сходимость рядов.
- •39 Знакочередующиеся ряды. Теорема Лейбница
- •40 Свойства абсолютно и условно сходящихся рядов
- •41 Функциональные ряды, основные понятия
- •42 Равномерная сходимость функциональных рядов. Критерий равномерной сходимости. Теорема Вейештрасса
- •25.3. Свойства равномерно сходящихся рядов.
- •44 Степенные ряды. Теорема Абеля
- •45 Свойства степенных рядов
- •46 Ряд Тейлора. Теорема о единственности разложения функции в ряд Тейлора
- •47 Необходимое и достаточное условие разложимости функции в ряд Тейлора
- •48 Разложение в ряд Маклорена простейших функций
- •49 Приложения степенных рядов к приближенным вычислениям: а) вычисление значений функции; б) вычисление ои; в) решение диф. Уравнений
- •1Функции
- •50 Ряды Фурье. Разложение в ряд Фурье функций заданных на [- ], [0,2 ], [-l,l], а также чётных и нечётных функций, функций заданных на [0, ]
- •51 Ортогональные системы функций. Скалярное произведение функций
25 Поток векторного поля, его физический смысл
Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.
Пусть
поверхность S расположена
в поле ![]() скоростей
частиц несжимаемой жидкости с
плотностью ρ = 1.
Можно показать, что поток векторного
поля в этом случае равен
скоростей
частиц несжимаемой жидкости с
плотностью ρ = 1.
Можно показать, что поток векторного
поля в этом случае равен
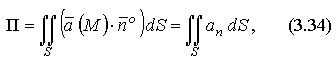
где ![]() –
единичный нормальный вектор к
поверхности S,
расположенный по одну сторону с
вектором
,
а величина
–
единичный нормальный вектор к
поверхности S,
расположенный по одну сторону с
вектором
,
а величина ![]() .
.
Независимо от физического смысла вектора интеграл (3.34) по поверхности называют потоком векторного поля через поверхность S.
Пусть ![]() и
и ![]() тогда
поток П вектора
через
поверхность S можно
записать в виде:
тогда
поток П вектора
через
поверхность S можно
записать в виде:
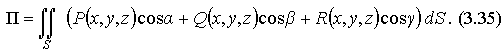
Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах:
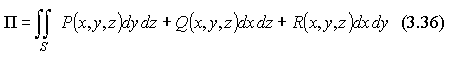
26 Дивергенция векторного поля, её свойства
Дивергенцией или расходимостью векторного поля называется скалярная функция, определяемая равенством:
![]()
На этот раз векторное поле порождает скалярное поле div .
С учетом понятий дивергенции и потока векторного поля формулу Остроградскогоможно представить в форме:
![]()
т. е. поток векторного поля через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.
На
основании формулы (3.38) можно записать:  и,
переходя к пределу, стягивая V в
точку М (при
этом величина V → 0 ),
имеем:
и,
переходя к пределу, стягивая V в
точку М (при
этом величина V → 0 ),
имеем:
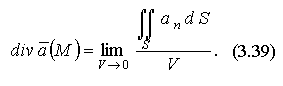
Отметим свойства дивергенции (справедливость которых рекомендуется показать самостоятельно):
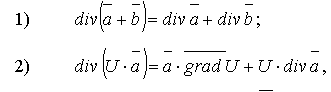
где U – скалярная функция.
27 Циркуляция векторного поля, её физический смысл
Циркуляцией
поля вектора ![]() по
данному контуру
по
данному контуру ![]() называется
предел интегральной суммы
называется
предел интегральной суммы ![]() ,
когда все
,
когда все![]() :
:
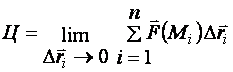 .
.
Данный
предел также называется криволинейным
интегралом вектора ![]() по
замкнутому контуру и обозначается
по
замкнутому контуру и обозначается 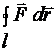 .
.
Таким образом,
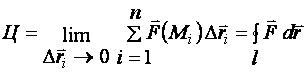
![]() .
(4)
.
(4)
Пусть
вектор ![]() физически
изображает силу, отнесенную к единице
длины. Тогда произведение
физически
изображает силу, отнесенную к единице
длины. Тогда произведение ![]() будет
изображать примерно величину силы
в точке
будет
изображать примерно величину силы
в точке ![]() .
Умножив её на
.
Умножив её на ![]() (
(![]() –
угол между
–
угол между ![]() и
и ![]() ),
получим проекцию этой силы на
направление
),
получим проекцию этой силы на
направление ![]() :
:
![]() .
В пределе вектор
.
В пределе вектор ![]() в
каждой точке
в
каждой точке ![]() направлен
по касательной к контуру
направлен
по касательной к контуру ![]() в
сторону положительного обхода.
Значит,
в
сторону положительного обхода.
Значит, ![]()
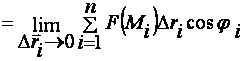 представляет
алгебраическую сумму сил, действующих
на контур по направлению касательной.
При этом положительные слагаемые (
–
острый угол) вращают контур в положительном
направлении. Если циркуляция положительная,
контур вращается в положительном
направлении, если циркуляция отрицательная
– в отрицательном направлении, если
циркуляция равна нулю (это возможно,
когда поле во всех точках контура
перпендикулярно к контуру или суммы
положительных и отрицательных слагаемых
одинаковы) – контур вращаться не будет.
представляет
алгебраическую сумму сил, действующих
на контур по направлению касательной.
При этом положительные слагаемые (
–
острый угол) вращают контур в положительном
направлении. Если циркуляция положительная,
контур вращается в положительном
направлении, если циркуляция отрицательная
– в отрицательном направлении, если
циркуляция равна нулю (это возможно,
когда поле во всех точках контура
перпендикулярно к контуру или суммы
положительных и отрицательных слагаемых
одинаковы) – контур вращаться не будет.
28 Ротор векторного поля, его свойства
Ротор (вихрь) векторного поля
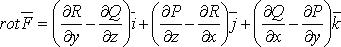
или в символическом виде
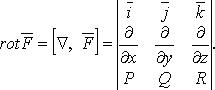
Свойства
ротора
![]()
![]()
![]()
