
- •1 Фигура, диаметр, мера. Определённый интеграл по фигуре (определение)
- •2 Масса фигуры переменной плотности
- •3 Геометрический смысл ди (двойного интеграла)
- •4 Геометрический смысл Кр и -1
- •5 Свойства определённого интеграла по фигуре
- •6 Вычисление криволинейного интеграла 1-ого рода
- •7 Вычисление ди в декартовых координатах
- •8 Вычисление ди в полярных координатах
- •9 Вычисление тройного интеграла в декартовых координатах
- •10 Вычисление Тройного интеграла в цилиндрических координатах
- •11 Вычисление тройного интеграла в сферических координатах
- •12 Вычисление пи-1
- •13 Вычисление статических моментов фигуры
- •14 Вычисление координат центра тяжести фигуры
- •15 Вычисление моментов инерции фигуры
- •Связь между криволинейными интегралами 1 и 2 рода.
- •17 Формула Грина
- •18 Независимость Кр и-2 от пути интегрирования
- •20. Формула Стокса
- •21 Формула Остроградского-Гаусса
- •22. Скалярное поле. Линии и поверхности уровня скалярного поля. Производная по направлению.
- •23 Градиент, свойства градиента
- •24 Векторное поле, определение, векторные линии, труба
- •25 Поток векторного поля, его физический смысл
- •26 Дивергенция векторного поля, её свойства
- •27 Циркуляция векторного поля, её физический смысл
- •28 Ротор векторного поля, его свойства
- •29 Оператор Гамильтона, диф.Операции 1-го и 2-го порядка
- •30 Простейшие векторные поля: потенциальное, соленаидальное, гармоническое
- •31 Определение числового ряда, основные понятия. Необходимые и достаточные условия сходимости ряда
- •32 Свойства сходящихся числовых рядов
- •33 Необходимое условие сходимости ряда. Достаточное условие расходимости числового ряда
- •34 Признаки сравнения числовых рядов
- •35 Признак д'Аламбера
- •36 Радикальный признак Коши
- •37 Интегральный признак сходимости
- •38 Знакопеременные ряды. Абсолютная и условная сходимость. Достаточное условие абсолютной сходимости знакопеременного ряда
- •24.2. Абсолютная и условная сходимость рядов.
- •39 Знакочередующиеся ряды. Теорема Лейбница
- •40 Свойства абсолютно и условно сходящихся рядов
- •41 Функциональные ряды, основные понятия
- •42 Равномерная сходимость функциональных рядов. Критерий равномерной сходимости. Теорема Вейештрасса
- •25.3. Свойства равномерно сходящихся рядов.
- •44 Степенные ряды. Теорема Абеля
- •45 Свойства степенных рядов
- •46 Ряд Тейлора. Теорема о единственности разложения функции в ряд Тейлора
- •47 Необходимое и достаточное условие разложимости функции в ряд Тейлора
- •48 Разложение в ряд Маклорена простейших функций
- •49 Приложения степенных рядов к приближенным вычислениям: а) вычисление значений функции; б) вычисление ои; в) решение диф. Уравнений
- •1Функции
- •50 Ряды Фурье. Разложение в ряд Фурье функций заданных на [- ], [0,2 ], [-l,l], а также чётных и нечётных функций, функций заданных на [0, ]
- •51 Ортогональные системы функций. Скалярное произведение функций
6 Вычисление криволинейного интеграла 1-ого рода
волинейный
интеграл![]() легко
сводится к определенному интегралу.
Примем за параметр длину дуги
легко
сводится к определенному интегралу.
Примем за параметр длину дуги![]() отсчитываемую
от точки А по кривой
отсчитываемую
от точки А по кривой![]() получим
параметрическое представление
кривой
получим
параметрическое представление
кривой![]() где
где![]() —
—
длина
дуги![]() Пусть
в (25.3) промежуточным точкам
Пусть
в (25.3) промежуточным точкам![]()
соответствует![]() т.е.
т.е.![]() Тогда
Тогда
![]()
Последняя
сумма является интегральной для
определения интеграла![]() т.е.
т.е.
![]() (25.4)
(25.4)
Эта
формула доказывает существование
криволинейного интеграла 1 рода от
функции![]() (х,у),
непрерывной в D, если
(х,у),
непрерывной в D, если![]() D
— непрерывная кусочно-гладкая кривая.
D
— непрерывная кусочно-гладкая кривая.
Рассмотрим формулы для вычислений криволинейного интеграла в следующих случаях:
а)![]() х
= x(t), у = y{t),
х
= x(t), у = y{t),![]() где
x{t) и y{t) непрерывно
где
x{t) и y{t) непрерывно
дифференцируемы
на![]() тогда
(см. разд. 18.3)
тогда
(см. разд. 18.3)
![]()
т.е. из (25.4) имеем
![]()
Формула
может быть обобщена на пространственный
случай, т.е. если![]() х
= x(t), у = y(t), z = z(t),
х
= x(t), у = y(t), z = z(t),![]() непрерыв-
непрерыв-
на
в D,![]() В,
тогда
В,
тогда
![]()
Аналогично записывается формула для большего числа переменных.
7 Вычисление ди в декартовых координатах


8 Вычисление ди в полярных координатах
Пусть область D записывается системой неравенств в полярных координатах:
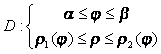
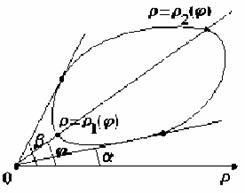
Такая область называется правильной в полярной системе координат, если каждый луч, выходящий из полюса, пересекает границу области не более, чем в 2-x точках.
По
определению 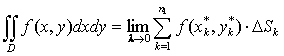 .
.
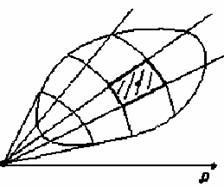
Т. к. значение двойного интеграла не зависит от способа разбиения области D на элементарные части, то сделаем это разбиение координатными линиями полярной системы координат (лучами из полюса и концентрическими окружностями).
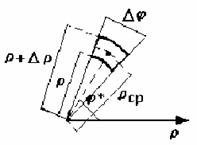
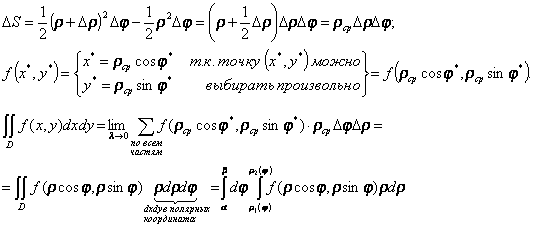
Переведенный
в полярные координаты двойной интеграл
сведен к повторному по имеющейся записи
области D неравенствами для переменных ![]() и
и ![]() .
В результате получаем формулу для
вычисления двойного интеграла в полярных
координатах:
.
В результате получаем формулу для
вычисления двойного интеграла в полярных
координатах:
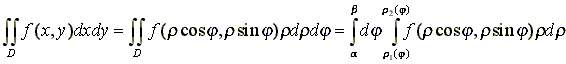 .
.
Обратите
внимание, что в правой части формулы
присутствует множитель ![]() -
это якобиан (определитель Якоби)
преобразования, который находится
следующим образом:
-
это якобиан (определитель Якоби)
преобразования, который находится
следующим образом:
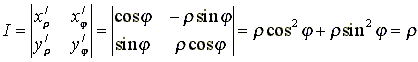
9 Вычисление тройного интеграла в декартовых координатах
Пусть
в трехмерной области V пространства OXY
задана функция ![]() .
Разобьем произвольным образом область
V на элементарные подобласти
.
Разобьем произвольным образом область
V на элементарные подобласти ![]() ,
в каждой подобласти зафиксируем
произвольную точку (
,
в каждой подобласти зафиксируем
произвольную точку (![]() )
и составим трехмерную интегральную
сумму
)
и составим трехмерную интегральную
сумму ![]() .
.
Тройным
интегралом от функции
по
ограниченной области V называется предел
последовательности соответствующих
интегральных сумм при стремлении к нулю
наибольшего из диаметров ![]() элементарных
областей
,
если этот предел не зависит ни от способа
разбиения области V на части, ни от выбора
точек
элементарных
областей
,
если этот предел не зависит ни от способа
разбиения области V на части, ни от выбора
точек ![]() :
:
![]() .
.
Вычисление
тройного интеграла сводится к вычислению
двойного интеграла и одного однократного
либо к вычислению трех повторных
интегралов. Если область V ограничена
сверху поверхностью ![]() ,
снизу поверхностью
,
снизу поверхностью ![]() ,
с боков – прямым цилиндром, вырезающим
на плоскости OXY область D, то
,
с боков – прямым цилиндром, вырезающим
на плоскости OXY область D, то  .
.
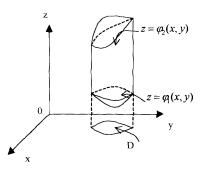
Рис. 9
С
помощью тройного интеграла объем тела,
изображенного на рис. 9, вычисляют по
формуле: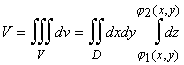 .
.
