48 Разложение в ряд Маклорена простейших функций
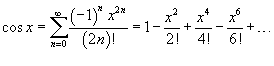
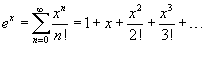
(1+x)m=1+
+
+
+
+…+
.
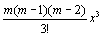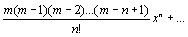49 Приложения степенных рядов к приближенным вычислениям: а) вычисление значений функции; б) вычисление ои; в) решение диф. Уравнений
1Функции
Продемонстрируем описанный метод на примере уравнения Кеплера
y = a + x sin y,
играющего важную роль в астрономии. Здесь y - эксцентрическая аномалия планеты, a - ее средняя аномалия, x - эксцентриситет орбиты планеты. Считая y неизвестной функцией от x, будем искать ее в виде
y = c0 + c1x + c2x2 + _
Разложив sin y по формуле (5) в ряд Тейлора по степеням y и подставив вместо y ряд (6), после возведения этого ряда в степени и приведения подобных членов получим
Из этого равенства, приравняв коэффициенты при одинаковых степенях x слева и справа, найдем последовательно неизвестные
и саму функцию
Доказано, что это разложение верно при | x | < < 0,6627_
2
Требуется вычислить интеграл: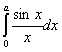
.
Разложим
подынтегральную функцию в ряд:из
равенства 
получаем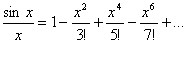 
это сходящийся ряд и мы его можем интегрировать почленно:
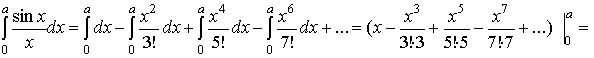
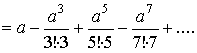Пусть a=0,8, тогда
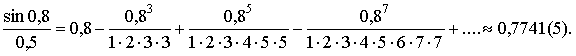
3 приближенного решения дифференциальных уравнений, обыкновенных и с частными производными. Не вдаваясь в сложные теоретические обоснования, рассмотрим дифференциальное уравнение Бесселя
x2y" + xy' + (x2 - n2)y = 0,
где n - постоянная (необязательно целая), x - независимая переменная, а y = y(x) - искомая функция. Решения этого уравнения, называемые функциями Бесселя, нашли применение практически во всех областях современного естествознания.
Будем искать y в виде обобщенного степенного ряда
где p, ak - неизвестные постоянные, причем a0 ? 0. Дифференцируя этот ряд дважды под знаком суммы, подставим выражения функции y и ее производных y', y" в уравнение (7). Затем сделаем приведение подобных членов, и коэффициенты полученного ряда приравняем нулю. После этого получим бесконечную систему уравнений
a0(p2 - n2) = 0, a1[(p + 1)2 - n2] = 0, ak[(p + k)2 - n2] + ak - 2 = 0, k = 2, 3, 4, _,
откуда находим p = ? n, a1 = a3 = a5 = _ = 0,
В случае нецелого n функции y1(x) и y2(x), соответствующие значениям p = n и p = - n, являются линейно-независимыми и любое другое решение дифференциального уравнения (7) имеет вид y = c1y1(x) + + c2y2(x), где c1 , c2 - постоянные. В случае целого n эти функции отличаются друг от друга только постоянным множителем, поэтому определяют лишь одно из двух линейно-независимых решений дифференциального уравнения.
50 Ряды Фурье. Разложение в ряд Фурье функций заданных на [- ], [0,2 ], [-l,l], а также чётных и нечётных функций, функций заданных на [0, ]
Ряд Фурье — представление произвольной функции f с периодом τ в виде ряда
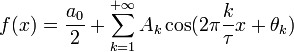Этот
ряд может быть также переписан в виде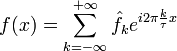
.
Где Ak — амплитуда k-го гармонического колебания,
—
круговая
частота гармонического колебания,
θk —
начальная фаза k-го
колебания,
— k-я
комплексная амплитуда
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x) .
Тогда для коэффициентов ее ряда Фурье находим формулы:
=
;
=
=
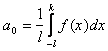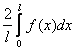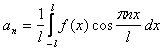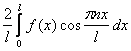
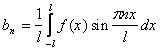0
,
где n=1,2,
...
Таким
образом, в ряде Фурье для четной функции
отсутствуют члены с синусами, и ряд
Фурье для четной функции с периодом
2L выглядит
так:
Пусть
теперь f(x)
- нечетная функция с периодом 2L,
удовлетворяющая условию f(-x)
= - f(x).Тогда
для коэффициентов ее ряда Фурье находим
формулы: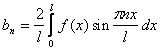
,
где n=1,2,
...Таким образом, в ряде Фурье для нечетной
функции отсутствует свободный член и
члены с косинусами, и ряд Фурье для
нечетной функции с периодом 2L выглядит
так:
Если
функция f(x)
разлагается в тригонометрический ряд
Фурье на промежутке
то 
,
где
,
,
,
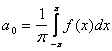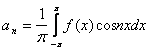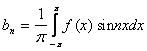Рядом
Фурье для функции
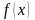в интервале
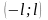называется тригонометрический ряд
,
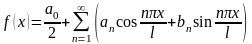(6)
где
коэффициенты ряда
,
,
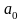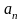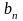(n=1,
2, 3,…) вычисляются по формулам Фурье:
;
(n=1,
2, 3,…); 
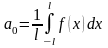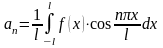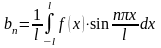(n=1,
2, 3,…). (9)