
- •1 Фигура, диаметр, мера. Определённый интеграл по фигуре (определение)
- •2 Масса фигуры переменной плотности
- •3 Геометрический смысл ди (двойного интеграла)
- •4 Геометрический смысл Кр и -1
- •5 Свойства определённого интеграла по фигуре
- •6 Вычисление криволинейного интеграла 1-ого рода
- •7 Вычисление ди в декартовых координатах
- •8 Вычисление ди в полярных координатах
- •9 Вычисление тройного интеграла в декартовых координатах
- •10 Вычисление Тройного интеграла в цилиндрических координатах
- •11 Вычисление тройного интеграла в сферических координатах
- •12 Вычисление пи-1
- •13 Вычисление статических моментов фигуры
- •14 Вычисление координат центра тяжести фигуры
- •15 Вычисление моментов инерции фигуры
- •Связь между криволинейными интегралами 1 и 2 рода.
- •17 Формула Грина
- •18 Независимость Кр и-2 от пути интегрирования
- •20. Формула Стокса
- •21 Формула Остроградского-Гаусса
- •22. Скалярное поле. Линии и поверхности уровня скалярного поля. Производная по направлению.
- •23 Градиент, свойства градиента
- •24 Векторное поле, определение, векторные линии, труба
- •25 Поток векторного поля, его физический смысл
- •26 Дивергенция векторного поля, её свойства
- •27 Циркуляция векторного поля, её физический смысл
- •28 Ротор векторного поля, его свойства
- •29 Оператор Гамильтона, диф.Операции 1-го и 2-го порядка
- •30 Простейшие векторные поля: потенциальное, соленаидальное, гармоническое
- •31 Определение числового ряда, основные понятия. Необходимые и достаточные условия сходимости ряда
- •32 Свойства сходящихся числовых рядов
- •33 Необходимое условие сходимости ряда. Достаточное условие расходимости числового ряда
- •34 Признаки сравнения числовых рядов
- •35 Признак д'Аламбера
- •36 Радикальный признак Коши
- •37 Интегральный признак сходимости
- •38 Знакопеременные ряды. Абсолютная и условная сходимость. Достаточное условие абсолютной сходимости знакопеременного ряда
- •24.2. Абсолютная и условная сходимость рядов.
- •39 Знакочередующиеся ряды. Теорема Лейбница
- •40 Свойства абсолютно и условно сходящихся рядов
- •41 Функциональные ряды, основные понятия
- •42 Равномерная сходимость функциональных рядов. Критерий равномерной сходимости. Теорема Вейештрасса
- •25.3. Свойства равномерно сходящихся рядов.
- •44 Степенные ряды. Теорема Абеля
- •45 Свойства степенных рядов
- •46 Ряд Тейлора. Теорема о единственности разложения функции в ряд Тейлора
- •47 Необходимое и достаточное условие разложимости функции в ряд Тейлора
- •48 Разложение в ряд Маклорена простейших функций
- •49 Приложения степенных рядов к приближенным вычислениям: а) вычисление значений функции; б) вычисление ои; в) решение диф. Уравнений
- •1Функции
- •50 Ряды Фурье. Разложение в ряд Фурье функций заданных на [- ], [0,2 ], [-l,l], а также чётных и нечётных функций, функций заданных на [0, ]
- •51 Ортогональные системы функций. Скалярное произведение функций
41 Функциональные ряды, основные понятия
Функциональные ряды
|
|
Определение. Если членами ряда будут не числа, а функции от х, то ряд называется функциональным.
Определение.
Частными
(частичными) суммами
функционального ряда
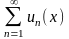 называются функции
называются функции
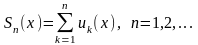
Определение.
Функциональный ряд
называется
сходящимся
в точке (х=х0),
если в этой точке сходится последовательность
его частных сумм. Предел последовательности
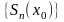 называется суммой
ряда
в точке х0.
называется суммой
ряда
в точке х0.
Определение. Совокупность всех значений х, для которых сходится ряд называется областью сходимости ряда.
Определение. Ряд называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
42 Равномерная сходимость функциональных рядов. Критерий равномерной сходимости. Теорема Вейештрасса
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда необходимо и достаточно, чтобы для любого числа >0 существовал такой номер N(), что при n>N и любом целом p>0 неравенство
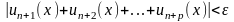
выполнялось бы для всех х на отрезке [a,b].
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд сходится равномерно и притом абсолютно на отрезке [a,b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
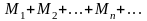
т.е. имеет место неравенство:
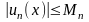 .
.
Еще
говорят, что в этом случае функциональный
ряд
мажорируется
числовым
рядом
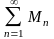 .
.
43 Свойства равномерно сходящихся рядов. Разложения в ряд функции arctg x для [x]<1
25.3. Свойства равномерно сходящихся рядов.
1) Теорема о непрерывности суммы ряда.
Если члены ряда - непрерывные на отрезке [a,b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a,b].
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке [a,b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a,b] , сходится к интегралу от суммы ряда по этому отрезку.
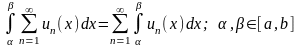
3) Теорема о почленном дифференцировании ряда.
Если
члены ряда
сходящегося на отрезке [a,b]
представляют собой непрерывные функции,
имеющие непрерывные производные, и ряд,
составленный из этих производных
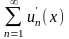 сходится
на этом отрезке равномерно, то и данный
ряд сходится равномерно и его можно
дифференцировать почленно.
сходится
на этом отрезке равномерно, то и данный
ряд сходится равномерно и его можно
дифференцировать почленно.
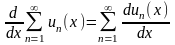
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
44 Степенные ряды. Теорема Абеля
Степенным рядом (ср.) называется ф.р. вида
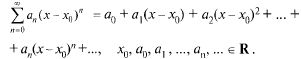 (30.1)
(30.1)
При![]() =
0 получаем ряд по степеням х.
=
0 получаем ряд по степеням х.
![]() (30.2)
(30.2)
Для того чтобы найти область сходимости ср., докажем теорему Абеля.
Т.
(Абеля): Если степенной ряд (30.2) сходится
при![]() то
он абсолютно сходится
то
он абсолютно сходится![]() Если
ряд (30.2) расходится в т.
Если
ряд (30.2) расходится в т.![]() то
он расходится
то
он расходится![]()
Пусть
ряд![]() сходится,
тогда
сходится,
тогда![]() Поскольку
Поскольку
функция,
имеющая предел, ограничена, то![]() Перепишем
ряд (30.2) в виде
Перепишем
ряд (30.2) в виде
![]()
Для ряда из абсолютных величин его членов
![]() (30.3)
(30.3)
имеем![]() >
причем геометрическая прогрессия
>
причем геометрическая прогрессия ![]() сходится
при
сходится
при![]() Таким
образом, при
Таким
образом, при![]() по
первому признаку сравнения ряд (30.3)
сходится, тогда по признаку абсолютной
сходимости ряд (30.2) сходится абсолютно.
по
первому признаку сравнения ряд (30.3)
сходится, тогда по признаку абсолютной
сходимости ряд (30.2) сходится абсолютно.
Пусть
теперь ряд (30.2) расходится при![]() Предположим
в противоречие с утверждением теоремы,
что
Предположим
в противоречие с утверждением теоремы,
что![]() при
котором ряд (30.2) сходится. Но по доказанному
выше ряд (30.2) должен тогда сходиться в
т.
при
котором ряд (30.2) сходится. Но по доказанному
выше ряд (30.2) должен тогда сходиться в
т.![]() Полученное
противоречие с условием доказывает
теорему
Полученное
противоречие с условием доказывает
теорему
