
- •25. Произведение двух многочленов с целыми коэффициентами.
- •26. Алгебраическая замкнутость поля.
- •27. Основная теорема алгебры.
- •28. Неприводимые над полем комплексных чисел многочлены.
- •29. Неприводимые над полем действительных чисел многочлены.
- •30. Решение уравнений 3 степени. Формулы Кардана.
- •31. Решение уравнений 4 степени. Кубическая резольвента.
- •32. Множество многочленов от нескольких переменных над областью целостности.
- •33. Кольцо многочленов от нескольких переменных над областью целостности.
- •34. Степень многочлена от нескольких переменных.
- •5. Степень произведения многочленов.
- •36. Лексикографическое упорядочение членов многочлена.
- •7. Лемма о высшем члене многочлена.
- •38.Свойства симметрических многочленов.
- •39.Элементарные симметрические многочлены. Теорема Виета.
- •40. Основная теорема о симметрических многочленах.
- •41. Условие при которых многочлены имеют общий корень
- •42. Результант многочленов Решение системы двух уравнений с двумя переменными с помощью результанта.
- •43. Необходимое и достаточное условие существования общего корня у многочленов
39.Элементарные симметрические многочлены. Теорема Виета.
Определение: элементарными симметрическими многочленами от переменных называются следующие многочлены:
 ;
;
 ;
;
 ;
;
………………………………………………………………………..
 ;
;
Существует связь элементарных симметрических многочленов с известными формулами Виета.
Теорема
(теорема
Виета):
пусть
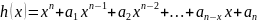 – многочлен кольца
и
– многочлен кольца
и –
корни этого многочлена, тогда:
–
корни этого многочлена, тогда:
 - (6)
- (6)
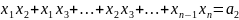 ;
;
 −
−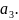
……………………………………………………………………..
 ;
;
До-во: так
как
–
корни многочлена
 то
то
 , выполнив умножение в правой части
и приравняв затем
, выполнив умножение в правой части
и приравняв затем
соответствующие коэффициенты правой и левой частей последнего
равенства, получим равенства (6) (формулы Виета).
до-но.
Согласно формулам
Виета значение симметрического
многочлена

 от корней многочлена
от корней многочлена
 равно коэффициенту
равно коэффициенту
 этого многочлена, взятому со знаком
этого многочлена, взятому со знаком

40. Основная теорема о симметрических многочленах.
Теорема (основная
теорема о симметрических многочленах):
всякий симметрический многочлен
из кольца
можно представить в виде многочлена
от элементарных симметрических
многочленов
 над полем
над полем
 ,
то есть
=g(
,
то есть
=g( ,
где
многочлен из кольца
[
].
,
где
многочлен из кольца
[
].
До-во: расположим члены многочлена в словарном порядке. Пусть при этом - (7) – высший член многочлена . По свойству 3 симметрических многочленов справедливы неравенства :
- (8)
Рассмотрим выражение
 - (9) .
- (9) .
Подберём показатели
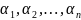 так,
чтобы высший член многочлена (9) совпал
с высшим членом многочлена
,
то есть с (7) .
так,
чтобы высший член многочлена (9) совпал
с высшим членом многочлена
,
то есть с (7) .
Высшими членами
многочленов
соответственно являются
,

 .
.
Тогда по лемме о высшем члене многочлена высшим членом многочлена (9) будет являться выражение :
 –(10);
–(10);
Это выражение совпадёт с (7) тогда и только тогда, когда будут выполняться равенства:






Из этой системы находим :
 ;
;
 ;
;
 ;
;
…………………….
 ;
;
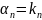 ;
;
Таким образом, высший член многочлена
 - (11)
- (11)
совпадает с высшим членом многочлена .
Вычтем из многочлена
многочлен (11). Пусть в результате получим
многочлен
,
то есть
 В результате вычитания высший член
многочлена
уничтожится
и все члены многочлена
будут
ниже (7).
В результате вычитания высший член
многочлена
уничтожится
и все члены многочлена
будут
ниже (7).
Пусть
 и
и
 –
(12) высший член многочлена
.
Вычтем далее из многочлена
многочлен
–
(12) высший член многочлена
.
Вычтем далее из многочлена
многочлен
 .
.
Получим

В результате
вычитания высший член многочлена
уничтожится и все члены многочлена
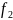 будут
ниже и т.д. Этот процесс понижения членов
многочленов не может продолжаться
бесконечно. Действительно, пусть на
каком-то
будут
ниже и т.д. Этот процесс понижения членов
многочленов не может продолжаться
бесконечно. Действительно, пусть на
каком-то
 -ом
шаге в результате вычитания мы
получим многочлен
-ом
шаге в результате вычитания мы
получим многочлен ,
высшим членом которого будет выражение
,
высшим членом которого будет выражение
 (13). По свойству
3 справедливы
неравенства
(13). По свойству
3 справедливы
неравенства
 .
При этом
.
При этом
 ≤
≤
 ,
так как член (13) ниже члена (7). Этим
условиям может удовлетворять лишь
конечное множество упорядоченных
систем целых неотрицательных чисел
,
так как член (13) ниже члена (7). Этим
условиям может удовлетворять лишь
конечное множество упорядоченных
систем целых неотрицательных чисел
 .
.
Таким образом , в конечном итоге будем иметь:
 ;
;
 ;
;
 ;
;
…………………………………………………….


= +…+
+…+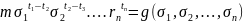 .
.
до-но.
Следствие: пусть
 – многочлен из кольца
– многочлен из кольца
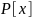 и пусть
– все корни этого многочлена. Тогда
всякий симметрический многочлен
из кольца
при
и пусть
– все корни этого многочлена. Тогда
всякий симметрический многочлен
из кольца
при
 ,
,
 ,
,
 принимает
значение принадлежащее полю
.
принимает
значение принадлежащее полю
.
